分極関数のはたらきを可視化する
Introduction
- 量子化学計算では、各原子上に配置した基底関数に分極関数を追加することで、電子分布が柔軟に変形する自由度を与えることができる
- p 軌道をもつ水素以外の原子に対しては、d 軌道タイプの関数を補助基底として追加
- s 軌道のみを持つ水素原子に対しては、p 軌道タイプ型の関数を追加
- 補助基底を追加することで、p 軌道と s 軌道のカタチが変えることができるという分極関数のはたらきを、いい感じで可視化したい
Results
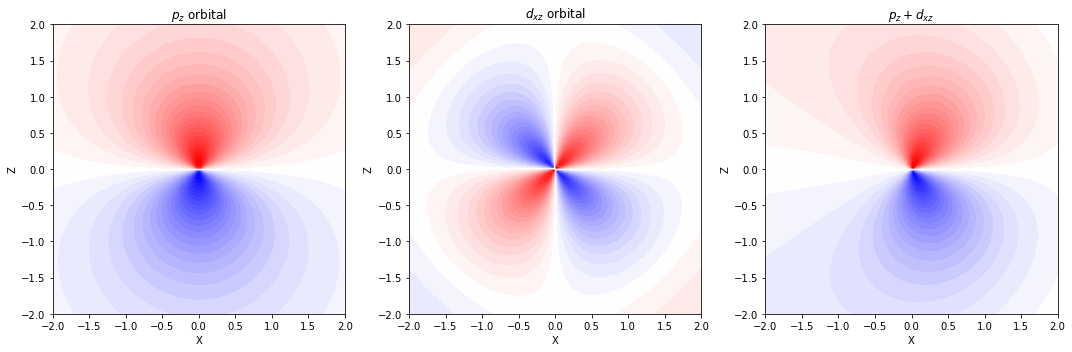
p軌道 + d軌道
p 軌道 : d 軌道 = 1.0 : 0.5のブレンド
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm
from matplotlib.colors import LinearSegmentedColormap
# Define the grid for x and z values
x = np.linspace(-2, 2, 100)
z = np.linspace(-2, 2, 100)
x, z = np.meshgrid(x, z)
# Convert from cartesian to spherical coordinates for xz-plane
r_values_xz = np.sqrt(x**2 + z**2)
theta_xz = np.arccos(z / r_values_xz)
phi_xz = np.arctan2(0, x) # y is 0 in xz-plane
# Compute the spherical harmonics values for p and d_xz orbitals in xz-plane
p_values_xz = sph_harm(0, 1, phi_xz, theta_xz).real
d_xz_values_xz = sph_harm(-1, 2, phi_xz, theta_xz).real
# Define the radial parts
def R_p(r):
return 2 * np.exp(-r)
def R_d(r):
return 2 * (1 - r/2) * np.exp(-r/2)
# Compute the radial values for original p orbital and adjusted d orbital in xz-plane
R_p_xz = R_p(r_values_xz)
R_d_xz = R_d(r_values_xz)
# Multiply the spherical harmonics by the radial functions in xz-plane
p_values_radial_xz = p_values_xz * R_p_xz
d_values_radial_xz = d_xz_values_xz * R_d_xz
# Combine the orbitals with a small weight for d_xz
combined_values_radial_xz = p_values_radial_xz + 0.5 * d_values_radial_xz
max_abs_p = np.max(np.abs(p_values_radial_xz))
max_abs_d = np.max(np.abs(d_values_radial_xz))
max_abs_combined = np.max(np.abs(combined_values_radial_xz))
levels_p = np.linspace(-max_abs_p, max_abs_p, 50)
levels_d = np.linspace(-max_abs_d, max_abs_d, 50)
levels_combined = np.linspace(-max_abs_combined, max_abs_combined, 50)
cm = LinearSegmentedColormap.from_list('custom_density', [(0, 0, 1), (1, 1, 1), (1, 0, 0)], N=256)
# Plotting with contours for xz-plane with adjusted orbitals
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
# Plot original p orbital
contour1 = ax[0].contourf(x, z, p_values_radial_xz, levels=levels_p, cmap=cm)
ax[0].set_title(r'$p_z$ orbital')
ax[0].set_xlabel("X")
ax[0].set_ylabel("Z")
# Plot adjusted d_xz orbital
contour2 = ax[1].contourf(x, z, d_values_radial_xz, levels=levels_d, cmap=cm)
ax[1].set_title(r'$d_{xz}$ orbital')
ax[1].set_xlabel("X")
ax[1].set_ylabel("Z")
# Plot combined orbital with original p and adjusted d_xz orbital
contour3 = ax[2].contourf(x, z, combined_values_radial_xz, levels=levels_combined, cmap=cm)
ax[2].set_title(r'$p_z + d_{xz}$')
ax[2].set_xlabel("X")
ax[2].set_ylabel("Z")
plt.tight_layout()
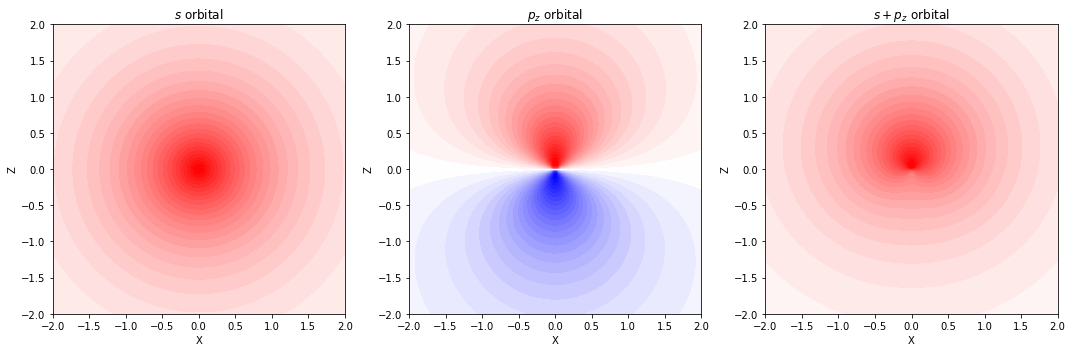
plt.show()s軌道 + p軌道
s 軌道 : p 軌道 = 1.0 : 0.1のブレンド
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm
from matplotlib.colors import LinearSegmentedColormap
# Define the grid for x and z values
x = np.linspace(-2, 2, 100)
z = np.linspace(-2, 2, 100)
x, z = np.meshgrid(x, z)
# Convert from cartesian to spherical coordinates for xz-plane
r_values_xz = np.sqrt(x**2 + z**2)
theta_xz = np.arccos(z / r_values_xz)
phi_xz = np.arctan2(0, x) # y is 0 in xz-plane
# Compute the spherical harmonics values for p and s orbitals in xz-plane
s_values_xz = sph_harm(0, 0, phi_xz, theta_xz).real
p_values_xz = sph_harm(0, 1, phi_xz, theta_xz).real
# Define the original radial part for p orbital and the radial part for s orbital
def R_p(r):
return 2 * np.exp(-r)
def R_s(r):
return np.exp(-r)
# Compute the radial values for original p orbital and s orbital in xz-plane
R_s_values_xz = R_s(r_values_xz)
R_p_values_xz = R_p(r_values_xz)
# Multiply the spherical harmonics by the radial functions in xz-plane
s_values_radial_xz = s_values_xz * R_s_values_xz
p_values_radial_xz = p_values_xz * R_p_values_xz
combined_values_radial_s_xz = s_values_radial_xz + 0.1 * p_values_radial_xz
# Define the contour levels
max_abs_s = np.max(np.abs(s_values_radial_xz))
max_abs_p = np.max(np.abs(p_values_radial_xz))
max_abs_combined = np.max(np.abs(combined_values_radial_s_xz))
levels_s = np.linspace(-max_abs_s, max_abs_s, 50)
levels_p = np.linspace(-max_abs_p, max_abs_p, 50)
levels_combined = np.linspace(-max_abs_combined, max_abs_combined, 50)
cm = LinearSegmentedColormap.from_list('custom_density', [(0, 0, 1), (1, 1, 1), (1, 0, 0)], N=256)
# Plotting
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].contourf(x, z, s_values_radial_xz, levels=levels_s, cmap=cm)
ax[0].set_title(r'$s$ orbital')
ax[0].set_xlabel("X")
ax[0].set_ylabel("Z")
ax[1].contourf(x, z, p_values_radial_xz, levels=levels_p, cmap=cm)
ax[1].set_title(r'$p_z$ orbital')
ax[1].set_xlabel("X")
ax[1].set_ylabel("Z")
ax[2].contourf(x, z, combined_values_radial_s_xz, levels=levels_combined, cmap=cm)
ax[2].set_title(r'$s + p_z$ orbital')
ax[2].set_xlabel("X")
ax[2].set_ylabel("Z")
plt.tight_layout()
plt.show()Conclusion
- できた