string 法に基づく最小エネルギー経路探索:エチレンが円錐交差点に辿り着くまで
前提
- string 法に基づく最小エネルギー経路(Minimum Energy Path; MEP)探索を行います
- 山本が Ruby で自作した
optpathというツールを使います - 京都大学化学研究所のスーパーコンピュータ(化研スパコン) で計算します
- 練習として、ethylene の S0→S1 Franck-Condon (FC) 点から S0/S1 Minimum Energy Conical Intersection (MECI) 点に至る MEP を探索します
- MEP 探索では「初期経路」が重要となるのですが、今回は、予め準備したものを使うことにします
- Python の Atomic Simulation Environment (ASE) パッケージを使って初期経路を作る方法があるので、後でまとめたいと思っています
- MEP 探索では「初期経路」が重要となるのですが、今回は、予め準備したものを使うことにします
- 量子化学計算プログラムとしては、計算手法にスピン反転時間依存密度汎関数理論(SF-TD-DFT)法を用いるので、これができる Q-Chem version 6.1 を使います
背景
- 最小エネルギー探索は、化学反応などにおいて、始状態(反応系)から終状態(生成系)に辿り着くまでのエネルギー変化が最も低くなるような経路を見つけるための手法です
- QM/MM 自由エネルギー摂動法を用いて自由エネルギー変化を解析しようとするときには、MEP を探索することが必要になります
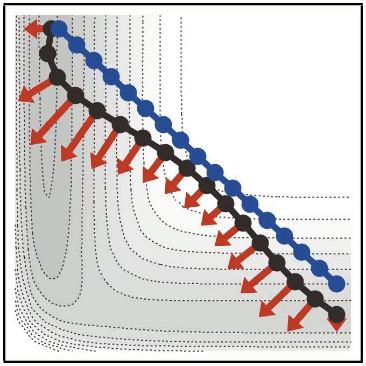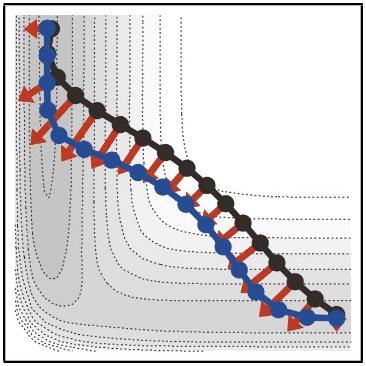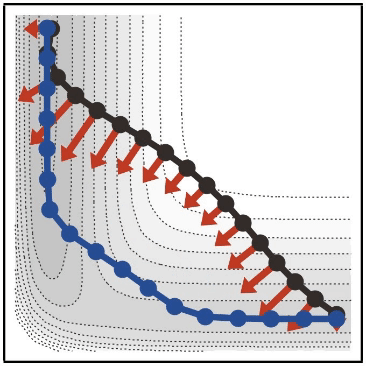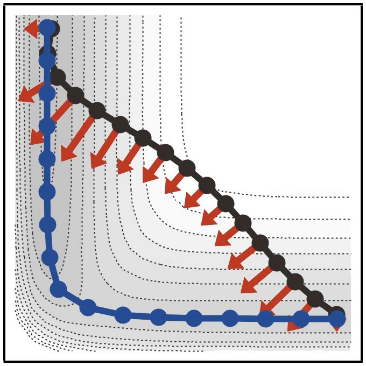
- string 法は、最小エネルギー探索手法の一つで、E や Vanden-Eijnden らによって開発されました(
論文
)
- 類似の方法としては、Nudged Elastic Band (NEB) 法などがあります(
論文
)
- NEB 法については、 Reaction plus という有料のソフトウェアや、 ASE という無料の Python ライブラリでも利用できます
- 類似の方法としては、Nudged Elastic Band (NEB) 法などがあります(
論文
)
- 山本が string 法について紹介した 日本語のレビュー もあるので、参考にしてみてください
準備
化研スパコンにログイン
sshコマンドを使って、自分のユーザーアカウント(例:yamnor)で化研スパコンfe1.scl.kyoto-u.ac.jpにログインします
ssh yamnor@fe1.scl.kyoto-u.ac.jpRuby をインストール
- 山本が自作した
optpathというツールは Ruby というスクリプト言語で書いています - 化研スパコンにインストールされている Ruby でも動作するのを確認しましたが、念のため、自分のホームディレクトリ(例:
/user1/scl9/yamnor)にインストールする方法もメモしておきます
準備
- 適当なディレクトリ(例:
~/tmp)に移動します
cd ~/tmpダウンロード
wget https://cache.ruby-lang.org/pub/ruby/3.3/ruby-3.3.1.tar.gz展開
tar xvfz ruby-3.3.1.tar.gzcd ruby-3.3.1設定
--prefixオプションで、Ruby のインストール先を指定します- ここでは、ホームディレクトリ(例:
/user1/scl9/yamnor)に作ったaplというディレクトリ内にインストールします- もし
aplがなければ、mkdir ~/aplで作っておきます
- もし
./configure --prefix=/user1/scl9/yamnor/apl/ruby-3.3.1コンパイル
- 4スレッド並列でコンパイルします
make -j 4インストール
- 指定したディレクトリ(
~/apl/ruby-3.3.1)にインストールされます
make installリンク
~/apl/rubyでアクセスできるように、リンクを作っておきましょう
cd ~/aplln -s ruby-3.3.1 ruby環境変数
- ログインシェルの設定ファイル(bashの場合は
.bashrc)に、下記の設定を追記します
export PATH=${HOME}/apl/ruby/bin:${PATH}
export RUBYLIB=${HOME}/apl/ruby/lib- 設定ファイルを再読み込み
source ~/.bashrcrubyにアクセスできるか確認
ruby -vruby 3.3.1 (2024-04-23 revision c56cd86388) [x86_64-linux]Ruby のライブラリをインストール
spliner
optpathは、経路を作るときに3次スプライン補間アルゴリズムを使っています- このための Ruby ライブラリをインストールします
gem install splineroptpath のインストール
- ホームディレクトリにある
aplというディレクトリに移動します
cd ~/aploptpathパッケージをダウンロードします
git clone https://github.com/yamnor/optpath.git練習ファイルをコピー
- ダウンロードした
optpathの中にある Q-Chem 用の練習ファイルを計算用のフォルダ(例:~/cal)にethyleneという名前でコピー
cp -r optpath/examples/qchem ~/cal/ethylene確認
- 以上で、ホームディレクトリにある
aplとcalは次のような構成になっているはずです
~/
├─apl
│ └─optpath
│ ├─examples
│ │ ├─gaussian
│ │ └─qchem
│ └─lib
└─cal
└─ethylene実行
準備
cal/ethyleneに移動します
cd ~/cal/ethylene- 中身を確かめてみます
ls- 下記の4つのファイルがあるはずです
optpath_in.rb path.xyz qm.grad qm.sng設定
optpathの設定は、optpath_in.rbで行います- ホームディレクトリの場所(例:
/user1/scl9/yamnor)を、自分の設定に合わせて書き換えてください
optpath.rb
#!/usr/bin/ruby
#PBS -q SMALL
#PBS -N ethylene
#PBS -l select=1:ncpus=12:mpiprocs=12:mem=48gb
#PBS -l walltime=12:00:00
##
# Path Optimization with the String Method
##
arg = {
#
# Input Files
#
path_xyz: "path.xyz",
#
qm_sng: "qm.sng",
qm_grad: "qm.grad",
#
# Setting of Path Optimization
#
stepsize: 1.0,
maxstep: 30,
nnodes: 12,
node_dir: "node",
node_log: "node.log.#{ENV['PBS_JOBID']}",
path_dir: "path",
path_log: "path.log.#{ENV['PBS_JOBID']}",
#
# Setting of QM Engine
#
qm_rootdir: "/usr/appli/qchem/610",
qm_scratch: "/scratch/qchem/#{ENV['PBS_JOBID']}",
#
qm_engine: "qchem",
qm_reptag: "__geom__", # ... replace the variables indicated by this tag
qm_input: "qm.inp",
qm_output: "qm.out",
qm_punch: "qm.dat",
qm_ncpus: 12,
}
$LOAD_PATH << '/user1/scl9/yamnor/apl/optpath/lib'
require 'pathoptimizer'
if ENV['PBS_O_WORKDIR'] != nil
Dir.chdir(ENV['PBS_O_WORKDIR'])
end
po = PathOptimizer.new(arg)
po.sng
po.run- string 法では、MEP に沿った各ノードで量子化学計算が必要となります
- Q-chem を用いた量子化学計算の設定は、エネルギー計算を
qm.sng、force の計算をqm.gradファイルで行います- 今回は、
qm.sngとqm.gradは全く同じ内容になります
- 今回は、
$molecule..$endブロックのなかで、optpathが分子の座標データを書き込む部分を__geom__タグで指定JOBTYPEには、forceを指定- あとは、一般的な量子化学計算の指定になります
- 今回は、S1 エネルギー曲面上で、FC 点 → MECI 点の MEP を求めます
- BHHLYP/6-31G(d) レベルで、スピン反転(spin-flip; SF)TD-DFT 計算をします
- SF-TD 法を用いるのは、CI 点近傍では、通常の TD 法だと破綻するから
- SF-TD 法の場合、出発点となる電子配置が三重項状態(T1)から、スピンを反転させることで、一重項基底状態(S0)や一重項励起状態(S1)を生成します
- S1は下から2つ目の状態になるので、
CIS_STATE_DERIVを2に指定
- S1は下から2つ目の状態になるので、
- このスクリプトでは、各ノードの量子化学計算を「並列」ではなく、「順番」に実行します
- 励起状態の計算にはコストが掛かるので、リソースを分散せずに、1つ1つの計算に集中しようという戦略
qm.sng/qm.grad
$molecule
0 3
__geom__
$end
$rem
JOBTYPE force
EXCHANGE bhhlyp
BASIS 6-31G(d)
SPIN_FLIP true
UNRESTRICTED true
CIS_N_ROOTS 3
CIS_STATE_DERIV 2
MAX_SCF_CYCLES 100
MAX_CIS_CYCLES 100
SYM_IGNORE true
$end- 初期経路の設定は、
path.xyzで行います- 始状態から終状態に至るまでの xyz 座標を並べて指定します
optpathで指定する離散点(ノード)の数と、ここで指定する座標の個数は一致していなくても大丈夫です- ミニマムには始状態と終状態の2個があればオーケーですが、
- MEP 探索では「初期経路」が重要ですが、今回は、予め準備したものを使うことにします
- 初期経路は ASE という Python ライブラリを使って準備することができるので、後日、紹介したいと思っています
path.xyz
6
image # 1 Energy = -78.52994
C 0.00518 0.00000 0.00112
C -1.31512 0.00001 0.00089
H -1.88398 -0.91658 0.00082
H -1.88398 0.91659 0.00079
H 0.57394 0.91665 0.00123
H 0.57395 -0.91668 0.00116
6
image # 2 Energy = -78.51896
C 0.05242 0.00098 -0.01644
C -1.36286 0.00481 -0.00058
H -1.88797 -0.91954 0.04787
(省略)
H -2.03783 0.69124 -0.49347
H 0.50978 0.40640 0.70127
H 0.53783 -0.74714 -0.44990
6
image # 18 Energy = -78.34789
C 0.08066 0.30221 -0.30377
C -1.27306 0.07886 -0.04672
H -1.69579 -0.66089 0.64517
H -2.06089 0.64923 -0.53641
H 0.53273 0.35454 0.71460
H 0.48635 -0.72393 -0.46686実行
qsub optpath_in.rb- ジョブの実行状況は、
qstatコマンドで確認できます
qstatJob id Name User Time Use S Queue
---------------- ---------------- ---------------- -------- - -----
2893390.fe3-adm ethylene yamnor 00:08:29 R SMALL- 計算が始まると、今回の設定では、
nodeとpathという2つのフォルダ、node.log.*とpath.log.*という2つのファイルができます
ethylene/
├─node/
├─node.log.2893390.fe3-adm
├─optpath_in.rb
├─path/
├─path.log.2893390.fe3-adm
├─path.xyz
├─qm.grad
└─qm.sngnodeには、各ノードでの Q-Chem の計算ログが残ります
node/
├─00
│ ├─qm.geom
│ ├─qm.grad
│ ├─qm.inp
│ └─qm.out
├─01
└─02
(省略)
├─09
├─10
└─11pathには、最適化している経路の情報が記録されます
path/
├─000.dat
├─000.grad
├─000.xyz
├─001.dat
├─001.grad
└─001.xyz
(省略)
├─030.dat
├─030.grad
├─030.xyz
└─sng.xyz*.datには、経路上の各ノードごとのポテンシャルエネルギーを記録します
030.dat
# Energy / au Delta-E / au Gradient / au DE / kcal mol-1
-78.3353613584 0.0000000000 0.0529956323 0.0000000000
-78.3716415974 0.0000000000 0.0005435334 -22.7661946372
-78.3741964515 0.0000000000 0.0003266565 -24.3693898411
-78.3792345117 0.0000000000 0.0004439576 -27.5308204999
-78.3859990766 0.0000000000 0.0008330186 -31.7756492086
-78.3928286549 0.0000000000 0.0016623470 -36.0612744495
-78.3984990789 0.0000000000 0.0005942788 -39.6195194280
-78.4018534843 0.0000000000 0.0019813852 -41.7244406387
-78.4016302569 0.0000000000 0.0021692475 -41.5843633247
-78.3998829011 0.0000000000 0.0021710707 -40.4878810030
-78.3893126226 0.0000000000 0.0011168969 -33.8549308363
-78.3573213260 0.0000000000 0.0179266038 -13.7800882546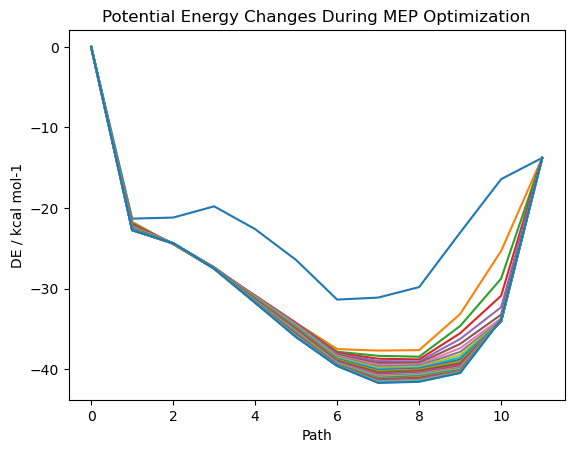
このファイルは、SF-TD 計算の参照状態、つまり、T1 のエネルギー変化が出力されるので、今回はあまり役に立たない情報になってしまっています
import matplotlib.pyplot as plt
import numpy as np
# データファイルの名前のリストを生成
filenames = [f"path/{i:03}.dat" for i in range(31)]
# 各ファイルからデータを読み込み、プロットする
for filename in filenames:
# ファイルからデータを読み込む
data = np.loadtxt(filename, skiprows=1) # ヘッダー行をスキップ
potential_energy_changes = data[:, 3] # 4列目のデータを取得
# データをプロット
plt.plot(potential_energy_changes, label=f"File {filename}")
# グラフの設定
plt.title('Potential Energy Changes During MEP Optimization')
plt.xlabel('Path')
plt.ylabel('DE / kcal mol-1')
plt.show()*.graには、経路上の各ノードで原子に掛かるエネルギー勾配の大きさを記録します
030.gra
6
C -0.2184073660 0.0000176576 -0.0000391570
C 0.2184259137 0.0000059386 0.0000392522
H 0.0001195234 -0.0040814767 -0.0000024149
H 0.0001206082 0.0040754422 0.0000023091
H -0.0001359842 0.0040930123 -0.0000022638
H -0.0001226951 -0.0041105742 0.0000022745
6
C -0.0016749522 -0.0000800634 0.0006689344
C 0.0016567148 -0.0000073016 -0.0002819993
H 0.0018830068 -0.0002684249 -0.0012523324
(省略)*.xyzには、経路上の各ノードにおける分子の座標を記録します
000.xyz
6
C 0.0051800000 0.0000000000 0.0011200000
C -1.3151200000 0.0000100000 0.0008900000
H -1.8839800000 -0.9165800000 0.0008200000
H -1.8839800000 0.9165900000 0.0007900000
H 0.5739400000 0.9166500000 0.0012300000
H 0.5739500000 -0.9166800000 0.0011600000
6
C 0.1069247886 0.0010471256 -0.0151659909
C -1.4163011623 -0.0002422812 0.0087023126
H -1.9487916403 -0.9294334570 0.0335358554
(省略)結果
nodeフォルダにある Q-Chem の出力ファイル(qm.out)かr、SF-TD 法で計算した S0 および S1 状態のエネルギーを読み取ることができます
qm.out
(省略)
---------------------------------------------------
SF-DFT Excitation Energies
(The first "excited" state might be the ground state)
---------------------------------------------------
Excited state 1: excitation energy (eV) = -4.1670
Total energy for state 1: -78.52286339 au
<S**2> : 0.0133
S( 2) --> S( 1) amplitude = 0.9899 alpha
Excited state 2: excitation energy (eV) = 0.9352
Total energy for state 2: -78.33536136 au
<S**2> : 2.0182
S( 1) --> S( 1) amplitude = 0.7107 alpha
S( 2) --> S( 2) amplitude = 0.6939 alpha
Excited state 3: excitation energy (eV) = 4.0106
Total energy for state 3: -78.22234102 au
<S**2> : 1.0134
D( 7) --> S( 1) amplitude = -0.9886
(省略)- 次のような Python スクリプトで、各ノードのエネルギーを読み取り、グラフにしてみます
import os
import matplotlib.pyplot as plt
# eVからkcal/molへの変換係数
ev_to_kcalmol = 23.06035
# フォルダ名を生成
folder_names = [f"node/{i:02}" for i in range(12)]
# エネルギー値を格納するリスト
energies_state1 = []
energies_state2 = []
# 各フォルダのファイルを読み込み
for folder in folder_names:
filepath = os.path.join(folder, "qm.out")
with open(filepath, 'r') as file:
energy_state1 = None
energy_state2 = None
for line in file:
if "Excited state 1: excitation energy (eV) =" in line:
energy_ev = float(line.split('=')[1].strip())
energy_kcalmol = energy_ev * ev_to_kcalmol # eVからkcal/molに変換
energy_state1 = energy_kcalmol
elif "Excited state 2: excitation energy (eV) =" in line:
energy_ev = float(line.split('=')[1].strip())
energy_kcalmol = energy_ev * ev_to_kcalmol # eVからkcal/molに変換
energy_state2 = energy_kcalmol
# 両方のエネルギーが見つかったらループを抜ける
if energy_state1 is not None and energy_state2 is not None:
break
energies_state1.append(energy_state1)
energies_state2.append(energy_state2)
# エネルギーの変化を計算(始点をゼロに設定)
delta_energies_state1 = [e - energies_state2[0] for e in energies_state1]
delta_energies_state2 = [e - energies_state2[0] for e in energies_state2]
# グラフをプロット
#plt.plot(delta_energies_state1, marker='o', label='S0', color='skyblue')
plt.plot(delta_energies_state2, marker='o', label='S1', color='orange')
plt.title('Energy Changes along the MEP')
plt.xlabel('Path')
plt.ylabel('ΔE (kcal/mol)')
#plt.ylabel('ΔE (eV)')
plt.legend()
plt.grid(True)
plt.show()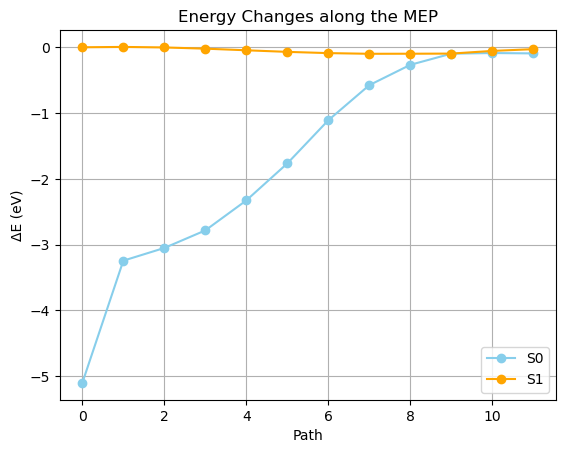
- S1状態だけをピックアップしてみると…
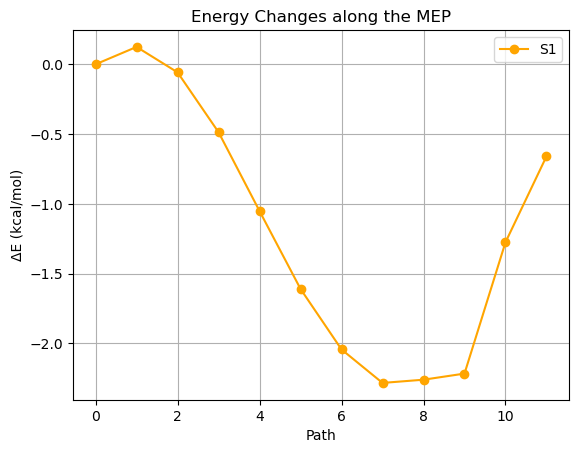
まとめ
- 今回は、string 法を使って、MEP を探索する手順について説明しました
- この解析に取り組むには、初期経路をどのように準備するのか?がカギになります
- 次は、ACE という Python ライブラリを使って、この初期経路を準備する方法を解説したいと思っています
- このパッケージを使うと、NEB 法を用いた MEP ができます
- ただし、SF-TD 法を用いるなど、込み入った計算には対応していないので、
optpathを使う利点はあるかなと思っています
このノートは、現在、アドレス(URL)を知っている人だけが閲覧できる「限定共有」版です。このページの URL は、関係者以外には秘密にしてください。