初歩から学ぶ!量子化学計算
概要
🧑🏫 講義① 10:30 〜 12:00
はじめに
学びの手引き
この資料について
- 資料は、講座が始まるまでに and/or 講座が終わってから、じっくりと読みながら学んでいただくことができるように準備しています
- 講座の終了後もできる限り公開を続けたいと思っていますが、事情により、公開先を変更することがあるかも知れません
この講座の進め方
- 時間が限られるので、講座では「ポイントのみを大まかに」という方針で、「量子化学計算をはじめようとするときに参考にしていただけそうな情報」をコンパクトにお伝えしたいと思っています
- 🟩 の項目は発展的な内容です
- 「はじめて量子化学計算に取り組もうとするとき」には、スキップしておいても良いように思います
- 今回は、🟩 の項目は「スキップ」する予定です
- スキップした内容のなかで、気になる項目があれば、お気軽にご質問ください
- 代表的なツールやアプリの「💻 実演」をおこないながら、「量子化学計算を実際におこなうときのイメージを掴んでいただくこと」も大切にしたいと思っています
- 当日は、疑問に思われたこと、詳細が知りたいと思われたこと、その他のこと、どんなことでも、Zoom の「Q&A ツール」からコメントをお送りください
- また、講座がはじまる前には、このサイトの左側に並ぶ「コメント」アイコンをクリックしてから、質問などを投稿していただくこともできます
- 以前開催したセミナーなどでいただいた「🤔 質問・コメント」も共有しています
🤔 事前質問・コメント
この講座の到達目標 🎯
- 量子化学計算に取り組むときに必要となる基礎的な知識と技術について、説明できる
- 代表的な量子化学計算ソフトウェアである Gaussian の特徴と基本的な計算手順 について、説明できる
- 量子化学の知識や技術に基づいて、おもに有機化合物の研究開発に応用するための指針について、説明できる
- 量子化学計算を活用して実験前の事前検証をおこない、研究・開発に必要となる時間的・資源的コストを効率化するための方針について、説明できる
この講座のタイムスケジュール ⏰
| 開始 | 終了 | 時間 | 内容 | |
|---|---|---|---|---|
| 10:30 | 12:00 | 90分 | 講義① | |
| 12:00 | 12:45 | 45分 | 🍱昼食 | |
| 12:45 | 14:15 | 90分 | 講義② | |
| 14:15 | 14:30 | 15分 | ☕休憩 | |
| 14:30 | 16:00 | 90分 | 講義③ | |
| 16:00 | 16:30 | 30分 | 🤔質疑 | |
| 16:30 | 🙇終了 |
🧑🏫 講義①
- はじめに
- 量子化学計算の概要
- 量子化学計算の代表的なソフトウェア
🧑🏫 講義②
- 量子化学計算の代表的な計算方法
- 量子化学計算の代表的な基底関数
🧑🏫 講義③
- 量子化学計算に基づく構造最適化
- 量子化学計算に基づく振動解析
- 量子化学計算に基づく化学反応の解析
- 🟩 量子化学計算に基づく電子励起状態の解析
- 🟩 量子化学計算に基づく溶媒効果の解析
🤔 質疑
- 質疑応答
- さいごに
参考書
この講座にぴったりの参考書 📘



量子化学計算の基礎を学ぶ 📘



量子化学計算をもっと深く学ぶ 📘



量子化学計算の概要
💻 実演:量子化学計算は手軽に実行できます
量子化学計算を使ってできること
分子の安定な構造を予測できます
分子の振動状態を予測できます
分子の励起状態を予測できます
分子の電子状態に基づいて様々な解析ができます
分子の化学反応を予測できます
🤔 量子化学計算が「できないこと」は?
- 一般に、「量子化学計算」と分類されたり、イメージされるプログラムや計算方法では、分子が数個〜十数個集まった系の計算が得意です
- 生体分子など、かなり大きな系でも量子化学計算ができるようになってきましたが、このような大きな系を扱おうとする場合には、立体構造をどのように準備するのか?が難しくなります
- 多くの場合、分子動力学シミュレーションなどと組み合わせて、適切な構造をサンプリングするなど、量子化学計算以外のツールも必要になります
分子シミュレーション手法の比較
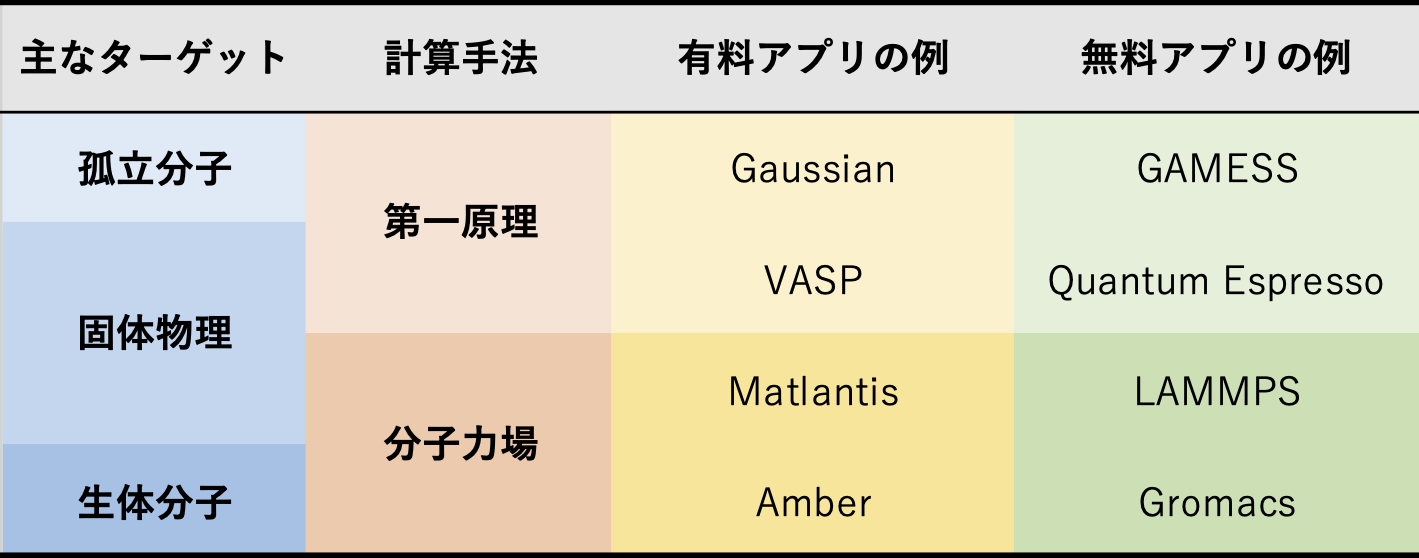
孤立分子 ➡ 量子化学計算
固体物理
- VASP
- Quantum Espresso
- Matlantis
- 第一原理計算のデータを深層学習したニューラルネットワークポテンシャル(NNP)力場を用います
- LAMMPS
生体分子
🤔 化合物が固体状態でも反応予測は可能?
- 化合物が固体状態の場合、もし量子化学計算で扱おうとする場合には、一部を切り出したモデル系として扱うことが多いです(「クラスターモデル」と呼ぶことがあります)
- 固体であることの物性(バンド構造など)が重要となる場合には、「固体物理」の分野でよく用いられている、 Quantum Espresso などの電子状態計算プログラムをつかったほうが、解析が進むかも知れません
- また、動的なふるまいに興味があったり、構造の揺らぎなどを詳しく知りたいときには、 LAMMPS などの分子動力学シミュレーションなどを利用する必要があるかも知れません
🤔 金属やPETなどの各材質への吸着性を数値化して算出することは可能?
🎈 応用事例: Amber を用いた分子動力学シミュレーション

🤠 力試し Quiz
「新薬を開発するケース」について、量子化学計算を用いることが適切だと思われるものをすべて選んでください。
- 新薬を設計するときに、薬物候補化合物として有力な幾つかの分子を合成する準備として、合成経路の素反応のひとつについて、対応する遷移状態のエネルギーを知りたい。
- 新薬を設計するときに、薬物候補化合物として有力だと思われる幾つかの分子について、分子内でどのような電荷分布になっているのか知りたい。
- 新薬を設計するときに、100 万個の化合物データベースの中から、薬物候補化合物としてふさわしい分子を1000 個選びたい。
- 新薬を設計するときに、薬物候補化合物として有力だと思われる幾つかの分子の赤外吸収スペクトルについて、それぞれのピークがどのような振動モードに由来するのかを調べたい。
- 新薬を設計するときに、薬物候補化合物として有力だと思われる幾つかの分子について、どのような結晶構造になっているのかを予測したい。
量子化学計算の代表的なソフトウェア 📀
業界標準の Gaussian
- 量子化学計算の プログラムは数多くある が、デファクトスタンダード(事実上の業界標準) は Gaussian
- 1970年に John A. Pople
(1998年ノーベル化学賞受賞)らが最初のバージョン(Gaussian 70)を開発
- Pople は、 いろいろあって 、Gaussian の使用を拒否されてしまったようです
- 名前は、分子軌道を表現するために用いる ガウス関数(Gaussian) に由来
- ガウス関数:$\exp(-\alpha r^2)$
- スレーター関数:$\exp(-\gamma r)$
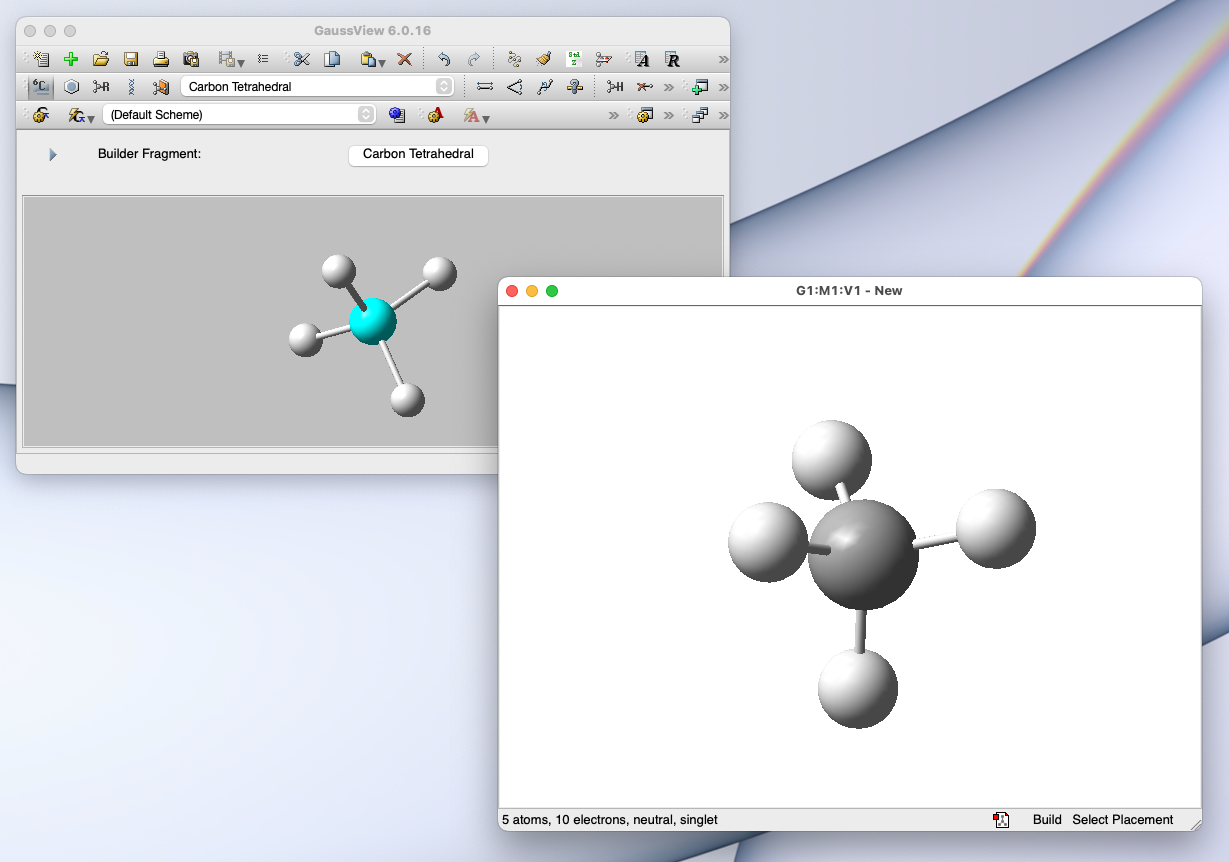
GaussView:ユーザーインターフェース
- GaussView というアプリと併せて使うと、高機能な量子化学計算をお手軽に実行できる
Gaussian の特徴
- 計算化学者だけではなく、実験化学者にも Gaussian ユーザーが多い
- 分からないこと・困ったことがあるとき、適切なアドバイスをしてくれるユーザーがすぐに見つかる
- インターネットの検索で有益な情報をたくさん得ることができる
- 最新版は Gaussian 16
- ライセンス方針が厳しい
- エネルギー計算 や 構造最適化 の収束性が良い
- 山本は、他の量子化学計算プログラムを使うときにも、構造最適化だけは Gaussian で実行する ことがあります
Gaussian の入力ファイル 📄
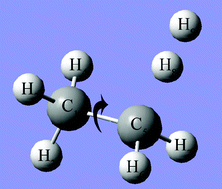
- 例:エチレン($\mathsf{C_2H_4}$)の構造最適化
#P HF/6-31G(d) Opt
C2H4
0 1
C 0.00000000 0.65855185 0.00000000
H 0.91494130 1.22519288 0.00000000
H -0.91468738 1.22560572 0.00000000
C 0.00000000 -0.65855185 0.00000000
H -0.91494130 -1.22519288 0.00000000
H 0.91468738 -1.22560572 0.00000000💻 実演:Gaussian/GaussView を用いた量子化学計算
Gaussian を販売している国内代理店 🏢
無料で使える GAMESS
- GAMESS は、Gaussian に次ぐ規模での利用実績がある
- General Atomic and Molecular Electronic Structure System の頭文字
- アメリカ版(GAMESS-US)、イギリス版(GAMESS-UK)、Firefly という3つの異なるバージョンがある
- GAMESSと言うとき、アメリカ版(GAMESS-US) を指すことが多い
- どのバージョンも、1970年代後半にアメリカ・エネルギー省の NRCC(National Resource for Computational Chemistry) というプロジェクトで開発されたプログラムコードが共通の先祖
- 1981年
- オリジナル版 GAMESS が アメリカ版(GAMESS-US) と イギリス版(GAMESS-UK) に枝分かれ
- 1997年
- アメリカ版(GAMESS-US)を元にして ロシアで Firefly の開発がはじまった
- この3つの異なるバージョンの GAMESS は、別々のグループで開発されている
- 各グループで独立に、より効率的に計算できるように改良、新しい機能が追加
- 現在では、お互いに全く異なる性質のものに
アメリカ 🇺🇸 版 GAMESS
- GAMESS-US
- アイオワ州立大学(アメリカ)の Mark Gordon の 研究室 が中心に開発
- 学術&商用で 無償利用可
- ➡ 商用でも無償という点は大きい!
- オープンソース ではない
- プログラムの再配布やソースコードの再利用は禁止
- GAMESS-US を利用した研究成果を公表する場合、開発者らによる下記の 原著論文
を引用する
- G. M. J. Barca, et al., J. Chem. Phys., Vol. 152, 154102 (2020)
- アップデートが頻繁なので、バージョン番号ではなく、更新日で管理 されている
- 最先端で開発が進められている 様々な新しい手法 を実行できる
- ソースコード を無償で入手することができる
- オリジナルの機能を自分で追加する ことができる
GAMESS-US の入力ファイル 📄
- エチレン($\mathsf{C_2H_4}$)の構造最適化
$CONTRL
SCFTYP=RHF
RUNTYP=OPTIMIZE
ICHARG=0
MULT=1
COORD=CART
$END
$BASIS
GBASIS=N31 NGAUSS=6 NDFUNC=1
$END
$DATA
C2H4
C1 1
C 6 0.00000000 0.65855185 0.00000000
H 1 0.91494130 1.22519288 0.00000000
H 1 -0.91468738 1.22560572 0.00000000
C 6 0.00000000 -0.65855185 0.00000000
H 1 -0.91494130 -1.22519288 0.00000000
H 1 0.91468738 -1.22560572 0.00000000
$ENDこの講座では
- 今回は主に、最も利用者が多い Gaussian について説明します
- GAMESS の「商用利用でも無償」というメリットは大きいのですが、Gaussian に比べると、利用者は少ないように思います
- GAMESS に言及する場合には、3種類のなかで最も代表的なアメリカ版(GAMESS-US)について説明します
🟩 量子化学計算を実行できるスパコン
- 自然科学研究機構 岡崎共通研究施設 計算科学研究センター
- 学術利用のみです
- 東京工業大学 学術国際情報センター スーパーコンピュータ TSUBAME 3.0
- 産業利用枠もあります
- 公益財団法人 計算科学振興財団 FOCUS スパコン
- 産業利用をメインにした計算環境です
🟩 実演:スパコンを用いたエタノールの量子化学計算
🟩 量子化学計算を体験できる Web アプリの MolCalc
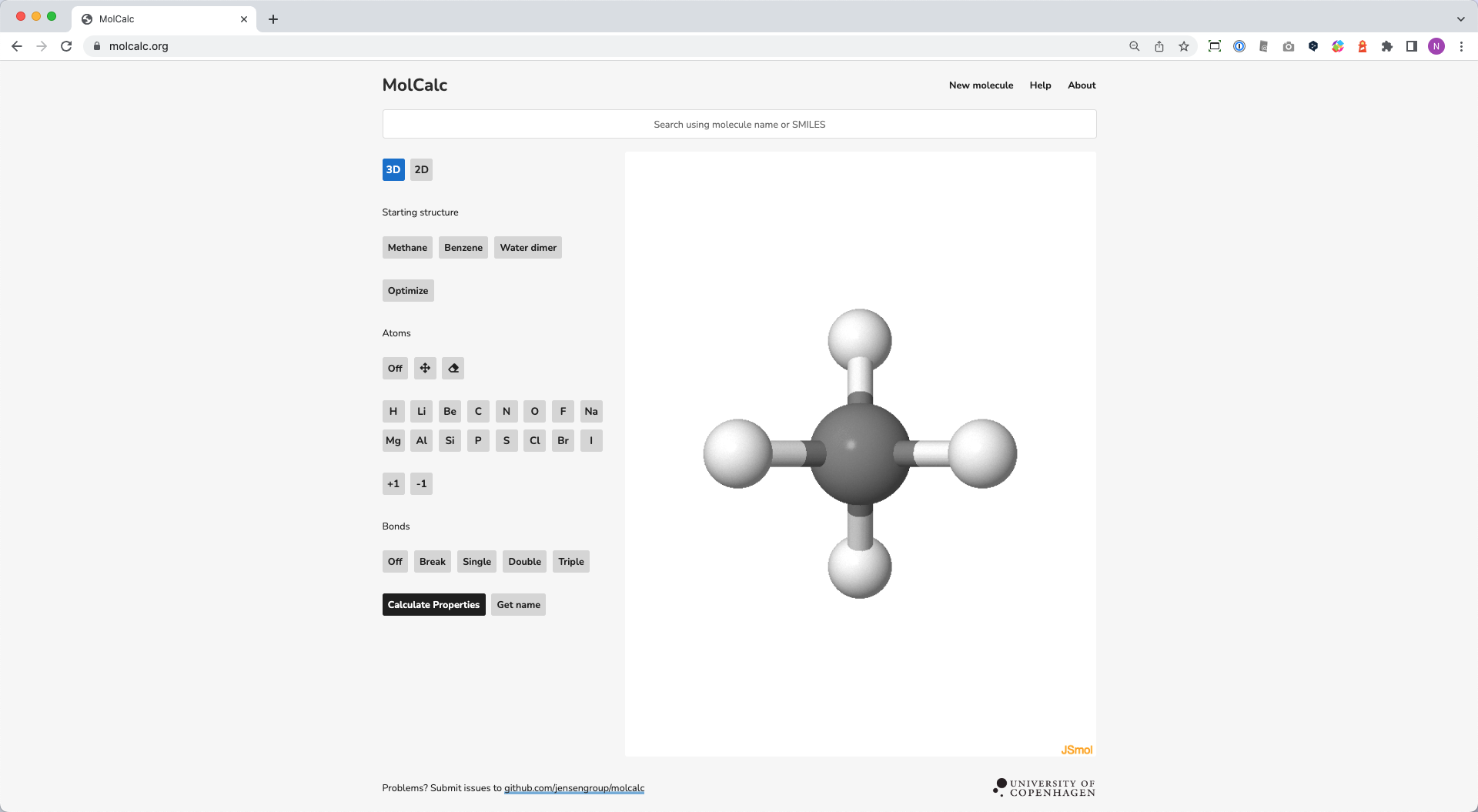
- 量子化学エンジンは GAMESS
- 計算レベルは
HF/STO-3G- 計算手法:Hartree-Fock 法
- 基底関数:STO-3G
- 開発者は Copenhagen 大学の Jan Jensen ら
- 分子を SMILES 記法で指定できる
- SMILES記法とは?
- 分子の化学構造を 文字列化 して表現する表記方法
- Simplified Molecular Input Line Entry System の頭文字
- 基本的なルール
- 原子は 元素記号 で表し、水素原子 は 省略 する
- 二重結合 は「
=」、三重結合 は「#」で表す - 単結合 は(通常は)省略 する
- 環構造 は、つながっている原子の後ろに数字でラベル付け する(
C1など)- 例:プロパン:
CCC、シクロプロパン:C1CC1
- 例:プロパン:
- 芳香環 を構成する原子は小文字にする(c など)
- 例:ベンゼン:
c1ccccc1
- 例:ベンゼン:
- SMILES 記法についての詳細は こちら
| 化合物名 | 化学式 | SMILES |
|---|---|---|
| メタン | CH4 | C |
| アンモニア | NH3 | N |
| 水 | H2O | O |
| 二酸化炭素 | CO2 | O=C=O |
| 窒素 | N2 | N#N |
| 酸素 | O2 | O=O |
| エタン | C2H6 | CC |
| エチレン | C2H4 | C=C |
| アセチレン | C2H2 | C#C |
| ブタン | C4H10 | CCCC |
| 1,3-ブタジエン | C4H6 | C=CC=C |
| 1,2-ブタジエン | C4H6 C=C=CC | |
| シクロブタン | C4H8 | C1CCC1 |
| シクロブタジエン | C4H4 | C1=CC=C1 |
| シクロヘキサン | C6H12 | C1CCCCC1 |
| シクロヘキセン | C6H10 | C1CCC=CC1 |
| 1,4-シクロヘキサジエン | C6H8 | C1C=CCC=C1 |
| ベンゼン | C6H6 | c1ccccc1 |
🟩 実演:MolCalc を用いたエチレンの量子化学計算
- SMILES 記法で分子を指定する
C=Cと入力する
- 分子が表示されたら、
Calculate PropertiesをクリックIndeedをクリック- 量子化学計算がはじまる
- 計算が終わったら、調べたい性質のタブをクリック
Free Energies:熱力学物性Vibrational Frequencies:振動解析Molecular Orbitals:分子軌道Polarity and Solvations:静電ポテンシャルや双極子モーメントなど
Gaussian や GAMESS を便利に使うための WebMO
- WebMO
- Web アプリ
- ブラウザーから量子化学計算を実行できる
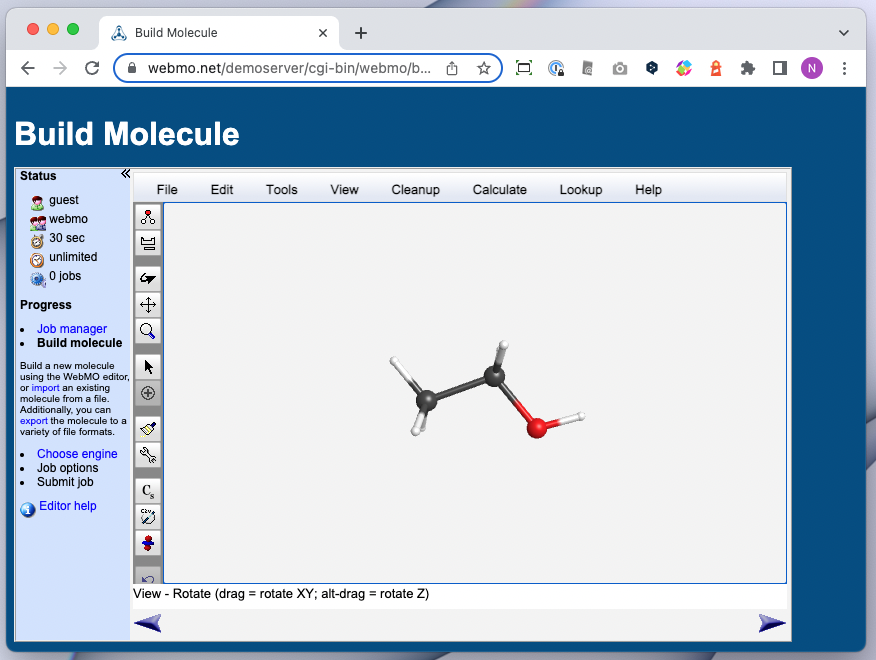
- 様々な量子化学計算パッケージのインターフェースとして使える
- Gaussian / GAMESS / Molpro / Mopac / NWChem / ORCA / PSI4 / Quantum Espresso / Q-Chem / VASP
- 公式サイトの デモ版
- Username:
guest - Password:
guest - 30秒までの計算が可能
- タイミングが悪いと混んでいる
- Username:
- 分子を SMILES で指定するときには、メニューから…
Lookup→Import by→SMILES- SMILES 記法
💻 実演:WebMO を用いたエチレンの量子化学計算
量子化学計算のコスト 💰
量子化学計算プログラム 💰
GUI アプリ 💰
- GaussView
- 学術:約 16 万円
- 商用:約 30 万円
- WebMO Basic
- 学術 / 商用:0 円
- WebMO Pro
- 学術:1,200 USD(約 16 万円)
- 商用:3,000 USD(約 41 万円)
計算用サーバー(クラウドサービス) 💰
- Sakura VPS
(CPU:仮想 8 core, メモリ:16 GB)
- 約 17 万円 / 年
- Amazon Web Service (AWS)
(CPU:仮想 8 core, 32 GBメモリ)
- 約 1.2 千円 / 日
コストを掛けずに量子化学計算をはじめる 💰
- ちょっと試す
- GAMESS + WebMO Basic + AWS
約 1.2 千円 / 日
- GAMESS + WebMO Basic + AWS
- もう少し本格的に
- GAMESS + WebMO Pro (商用) + Sakura VPS
約 17 万円 / 年+約 41 万円
- GAMESS + WebMO Pro (商用) + Sakura VPS
🍱 昼休憩 12:00 〜 12:45
🤔 ある特定の分子が結晶性を有するのかどうか、計算にて考察できますか?
- ある分子について、結晶構造を形成した場合の安定性を定量的に評価しようとする場合には、午前中に少しご紹介した「
Conflex
」などを利用していただく方がスムーズかと思います
- 分子力場モデルと呼ばれる計算手法を用いて、複数の候補構造を高速に計算することで、最も安定な結晶構造を予測することができます
- Gaussian で、1つの分子性結晶について詳しく量子化学計算することも可能です
- CIF ファイルをそのまま読み込ませて、周期性(Periodic Boundary Condition; PBC)を考慮した計算(構造最適化など)を行うことができます
- ただし、一般的な量子化学計算プログラム(Gaussian や GAMESS)は「周期性」を考慮した計算が効率的ではないので、時間が掛かってしまうことが多いです
🤔 GAMESS + WebMO Basic + AWSという組み合わせを具体的に行う方法は?
- 具体的なインストール方法は「
ここ
」が参考になるかと思います
- 手順としては、クラウド(AWS や Sakura VPS)で Web サービスが実行できるように設定した後、GAMESS と WebMO Basic をインストールします
- 量子化学計算を実行するときには、「メモリ」を比較的多く準備する必要があります
- 最低でも 4 GB 程度は必要かと思います
- AWS の設定などは少し面倒な部分もありますので、別途、技術相談などでお話をお伺いすることもできるかと思います
🧑🏫 講義② 12:45 〜 14:15
量子化学計算の代表的な計算方法
電子相関を考慮しない計算方法
- Hartree-Fock(HF)法
電子相関を考慮する計算方法
- 密度汎関数法
- 🟩 Møller-Plesset 摂動法(例:MP2, MP4)
- 🟩 結合クラスター法(例:CCSD, CCSD(T))
- 🟩 配置間相互作用(例:CISD, Full CI)法
💻 実演:Gaussian で利用できる様々な計算方法
代表的な計算方法の精度とコスト
Hartree-Fock 法とは?
シュレディンガー方程式
$$ \left[ -\frac{1}{2} \sum_i^n \nabla_i^2 + \sum_i^n v(r_i) + \sum_{i}^n \sum_{j > i}^n \frac{1}{\left| r_{i} - r_{j} \right|} \right] \Psi = E \Psi $$
- 2項目の $v(r_i)$ は、$i$ 番目の電子に外部(原子核)からはたらくポテンシャル $$ v(r_i) = -\sum_a^{N_\mathbf{nuclei}} \frac{Z_a}{|R_a - r_i|} $$
- 3項目の $\frac{1}{|r_{i}-r_{j}|}$ は、$i$ 番目と $j$ 番目の「電子間にはたらく相互作用(電子相関)」を表す
- 「ある電子は、他の電子の位置に依存しながら運動している」という描像(多電子描像)
- 厳密に取り扱うことが難しいため、何らかの「近似」が必要
- 「ある電子は、他の電子の位置に依存しながら運動している」という描像(多電子描像)
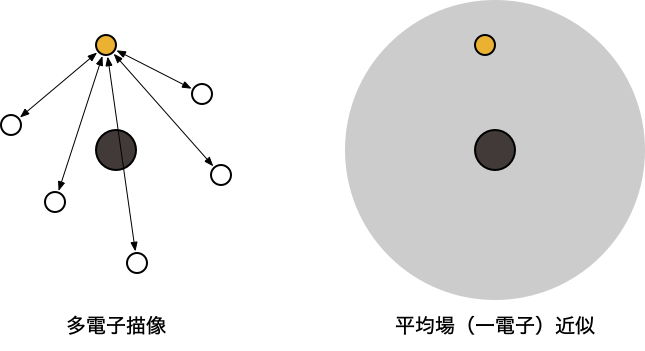
Hartree-Fock (HF) 方程式
- 量子化学計算の出発点となる最も基本的な近似
- 「ある電子は、他の電子の作る平均化された場の中で(他の電子と)独立に運動している」という描像(一電子近似)を考える

$$ \left[ -\frac{1}{2} \nabla_i^2 + v(r_i) + V_i^{\mathrm HF} \right] \psi_i = \epsilon_i \psi_i $$
- 3項目の $V_i^{\mathrm HF}$ は、$i$ 番目の電子に対して他の電子($j \neq i$)が作る「平均場」に由来する反発エネルギー
HF 法の計算例(He 原子の場合)
ステップ 1️⃣
- 対象とする分子系のハミルトニアン(核座標の配置 $R_\alpha$ 、核電荷 $Z_\alpha$、電子数 $n$ などの情報)、初期の参照軌道 $\Psi^{0}$ を設定する

- 対象とする分子系のハミルトニアン: $$ \hat{H} = -\frac{1}{2} \nabla_1^2 -\frac{1}{2} \nabla_2^2 - \frac{2}{r_1} - \frac{2}{r_2} + \frac{1}{r_{12}} $$
- 初期の参照軌道:
$$
\Psi^{0}(\xi_1,\xi_2)=\frac{1}{\sqrt{2}}\left[ \alpha(s_1)\beta(s_2) - \alpha(s_2)\beta(s_1)\right]\psi^{0}(r_1)\;\psi^{0}(r_2)
$$
- もちろん、ここにある $\psi^0(r_1)$ や $\psi^0(r_2)$ は、「これから求めたいもの」なので、その中身が分からない
- 拡張 Huckel 近似や半経験法など、精度の粗い方法をつかって、とりあえず求めておく
ステップ 2️⃣
- 「電子2がつくる平均場」中にある電子1について、HF 方程式を解く
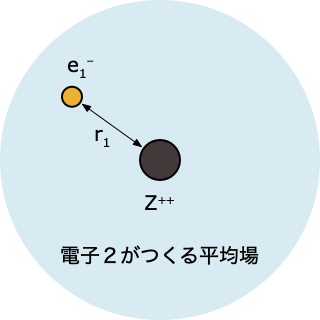
$$ \left[-\frac{1}{2}\nabla_1^2 - \frac{2}{r_1} + \int d r_2 \; |\psi^0(r_2)|^2 \, \frac{1}{r_{12}}\right]\psi(r_1)=\epsilon_1 \psi(r_1) $$
- これを解くと電子1の波動関数 $\psi(r_1)$ とエネルギー $\epsilon_1$ が求まるけれど、ステップ①で「とりあえず」ということで決めた $\psi^0(r_2)$ をつかった計算なので、精度的にはまだまだ不十分
ステップ 3️⃣
- 「電子1がつくる平均場」中にある電子2について、HF 方程式を解く
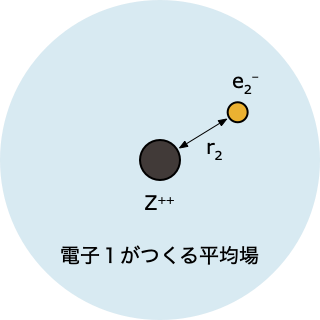
$$ \left[-\frac{1}{2}\nabla_2^2 - \frac{2}{r_2} + \int d r_1 \; |\psi^0(r_1)|^2 \, \frac{1}{r_{12}}\right]\psi(r_2)=\epsilon_2 \psi(r_2) $$
- これを解くと電子2の波動関数 $\psi(r_2)$ とエネルギー $\epsilon_2$ が求まるけれど、、ステップ①で「とりあえず」ということで決めた $\psi^0(r_1)$ をつかった計算なので、得られる答えも、精度的にはまだまだ不十分
ステップ 4️⃣
- 軌道エネルギー $\epsilon_i$ と1電子軌道 $\psi(r_i)$ から、全電子エネルギー $E$ を求める
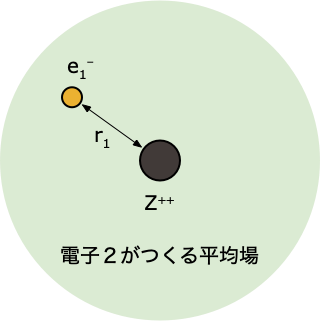
- ステップ②の続きでは、アップデートした $\psi^0(r_2)$ をつかった計算なので、得られる答えは、1回目よりも改善される(エネルギーが下がる)

- 得られた全エネルギー $E_\mathrm{new}$ と前回のもの $E_\mathrm{old}$ とのエネルギー差 $\Delta E$ を比べたときに…
- $\Delta E$ が十分に小さい
- ➡ 計算終了
- $\Delta E$ が大きい
- ➡ アップデートした軌道 $\Psi_\mathrm{new}$ を参照 $\Psi^0$ に使って、ステップ②〜④を再度実行
- $\Delta E$ が十分に小さい
Hartree-Fock 法の特徴
- 分子の立体構造や化学的性質について、多くの場合、十分な精度で予測できる
- 分子が最適構造にあるとき、その分子の全エネルギーの値を99%程度の精度で見積もることができる
- しかし、化学反応を議論するためには、99%程度という精度でも不十分であり、より高精度な予測が必要となる
- 化学反応に伴う活性化エネルギー $E_a$ を議論しようとする場合、$E_a$ は 20 kJ/mol 程度(5 kcal/mol 程度) になることが多いので、この程度以下の誤差となることが望ましい
- 電子相関を考慮するように HF 法を拡張し、HF 法以上の計算精度を持つ手法のことを「post Hartree-Fock 法」と呼ぶ
- post HF 法では、HF 法では無視してしまった「電子相関」の効果について、様々な工夫で考慮する
🤠 力試し Quiz
Hartree-Fock (HF) 法に関する次の文章について、適切なものをすべて選んでください。
- HF 法は、「ある電子について、他の電子の作る 平均化された場の(平均場) 中で、他の電子とは独立に運動している」という描像で近似している。
- HF 法は、電子同士の相互作用に由来する「電子相関」について、定量的な精度で十分に考慮することができる計算方法である。
- HF 法は、分子の立体構造や化学的性質について、多くの場合、十分な精度で予測できる。たとえば、全エネルギーの値についても、99%程度の精度で見積もることができる。
- HF 法は、化学反応に伴う活性化エネルギーについて定量的な精度で議論したい場合でも、十分に信頼できる結果が得られる計算方法である。
電子相関とは?
- Hartree-Fock 法は、電子同士の相互作用(電子相関)を平均化して扱うという近似(平均場近似)をしている

- 電子相関の大きさは「電子相関エネルギー」($\Delta E_\mathrm{corr}$)と呼ばれ、一般に、シュレディンガー方程式の厳密解($E_\mathrm{exact}$)と HF 計算で得られる値($E_\mathrm{HF}$)との差分として定義される
- $\Delta E_\mathrm{corr} = E_\mathrm{exact} - E_\mathrm{HF}$
電子相関の具体例
- 水分子1個の場合で、動的電子相関エネルギーは 140 kcal/mol 程度
- 動的電子相関を考慮する計算方法を用いると、動的電子相関に由来する誤差は…
- MP2 摂動法では 8 kcal/mol 程度
- CCSD(T) レベルでは 1 kcal/mol 以下
- 化学反応を定量的に議論することが可能な精度
電子相関を考慮する計算方法
- 密度汎関数法
- 🟩 Møller-Plesset 摂動法
- 二次の Møller-Plesset (MP2:second-order Møller-Plesset) 摂動法は、計算コストを比較的抑えながら電子相関の効果を大雑把ながらも比較的精度良く見積もることができる
- 生体分子など、大規模な分子系に対する電子相関補正として用いられることが多い
- 二次の Møller-Plesset (MP2:second-order Møller-Plesset) 摂動法は、計算コストを比較的抑えながら電子相関の効果を大雑把ながらも比較的精度良く見積もることができる
- 🟩 結合クラスター法
- 化学反応にともなうエネルギー変化に基づいて反応速度を議論したい場合など、高い定量性が求められる応用研究に多く利用されてるのは、結合クラスター法を用いた CCSD(T) レベル
- ただし、計算手法が高度になるほど、計算するためのコスト(計算に必要な時間やコンピュータの性能)も大きくなってしまうことがほとんどなので、目的に見合った精度とコストのバランスを考えることも大事になる
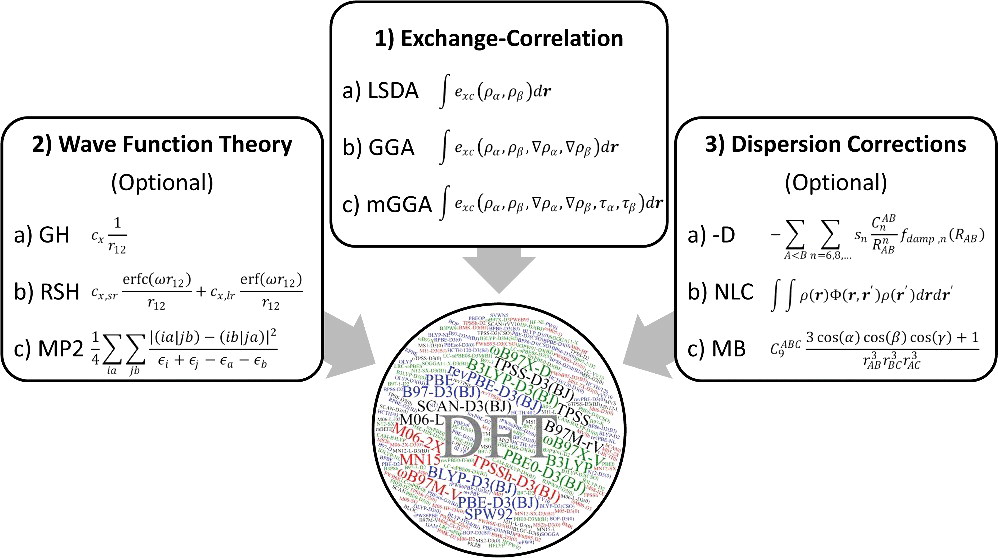
密度汎関数法(DFT:Density Functional Theory)とは?
- 近年、研究開発の最前線で大活躍している計算手法
- 電子密度を試行関数とする多電子状態問題の近似解法
- 電子相関の寄与について、 Hartree-Fock 法とほぼ同程度の計算コストで考慮することができる
- Hartree-Fock 法 などは波動関数を試行関数とする方法であるが、DFT は電子密度を試行関数とする方法であり、その基盤となる考え方が大きく異なっている
- HF 法の基礎は HF 方程式だが、DFTを実践する上で鍵になるのは コーン・シャム(Kohn-Sham; KS)方程式
Kohn-Sham 方程式とは?
Hartree-Fock 方程式
$$ \left[ -\frac{1}{2} \nabla_i^2 + v(r_i) + V_i^\mathrm{HF} \right] \psi_i = \epsilon_i \psi_i $$
- 3項目の $V^\mathrm{HF}$ は「ある電子-他の電子間の「平均」反発エネルギー」を表す
- 「ある電子は、他の電子の作る平均化された場の中で(他の電子と)独立に運動している」という描像
Kohn-Sham 方程式
$$ \left[ -\frac{1}{2} \nabla_i^2 + v(r_i) + V_i^\mathrm{eff} \right] \psi_i = \epsilon_i \psi_i $$
- 3項目の $V^\mathrm{eff}$ は、「外場有効ポテンシャル」
- $V^\mathrm{eff} = J + V_\mathrm{xc}$
- $J$:電子-電子間の古典的な静電(クーロン)相互作用
- $V_\mathrm{xc}$:非古典的な相互作用であり、(交換相関)汎関数と呼ばれる
- DFT を特徴付ける重要なもの
- このアイデアを大まかに説明すると…
- 外部有効ポテンシャル $V^\mathrm{eff}$ のもとにある $n$ 個の相互作用がない仮想の電子系(Kohn-Sham 系)を考える
- ただし $V^\mathrm{eff}$ は、相互作用を考慮したリアルな系で求められるものと等しい(仮想的な分子系) とする
🟩 Kohn-Sham 系のイメージ
Hartree-Fock 法と DFT 法(Kohn-Sham 法)の違い
- Kohn-Sham 方程式と Hartree-Fock 方程式の違いは、3項目が「平均場 $V^\mathrm{HF}$」か「外場有効ポテンシャル $V^\mathrm{eff}$」かのみ
- つまり、Kohn-Sham 方程式は、Hartree-Fock 方程式と同程度の時間で計算できる
- Hartree-Fock 方程式中の「平均場 $V^\mathrm{HF}$」は「既知の関数」であるが、Kohn-Sham 方程式中の「交換相関汎関数 $V_\mathrm{xc}$」は厳密な形が不明な「未知の関数」である
- $V_\mathrm{xc}$ の厳密な形が分からないので、人為的に仮定された汎関数を使う
- この 「人為的に仮定された」汎関数の質 が、DFT の精度を決定する
密度汎関数法で用いる「汎関数」
- DFT の計算精度と信頼性は、電子密度と系のエネルギーを関係付ける汎関数の種類に依存する
- 適切な汎関数を選べば、良い計算精度が得られる
Gaussian で利用できる様々な汎関数

交換・相関汎関数の分類
- 局所スピン密度近似(LSDA)型
- 電子密度 $\rho$ のみで表現された汎関数
- 一般化勾配近似(GGA)型
- LSDA を電子密度勾配 $\nabla \rho$ で補正した汎関数
- meta GGA 型
- GGA を運動エネルギー密度 $\tau$で補正した汎関数
- hybrid 型
- Hartree-Fock 交換積分 $E_\mathrm{x}^\mathrm{HF}$ を一定量混合した汎関数
🟩 交換・相関汎関数の大まかな分類
交換・相関汎関数の種類と計算精度
🟩 交換・相関汎関数の階層的な分類
- Perdew によって提案された汎関数の階層的な分類です。
- Jacob のはしご (Wikipedia) 、と呼ばれています。
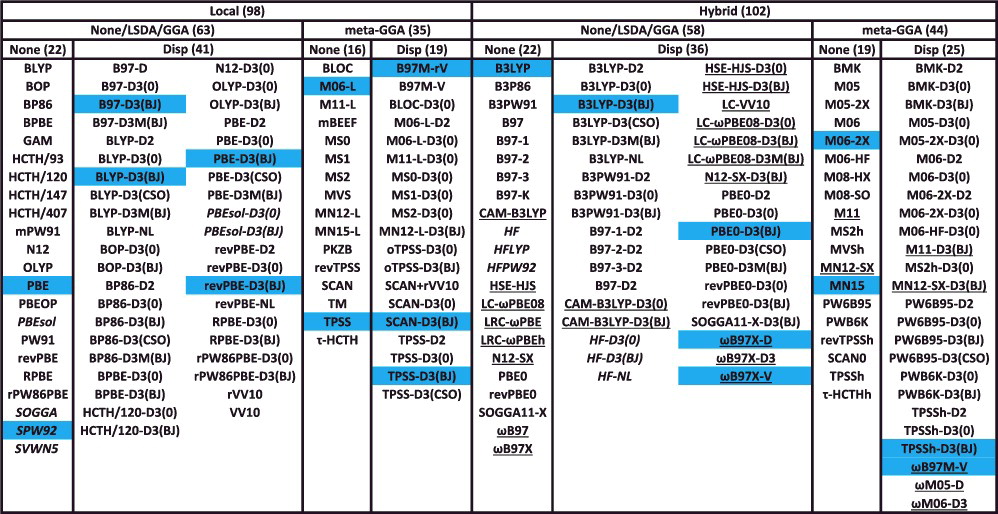
交換・相関汎関数の例
- 代表的な200個の交換・相関汎関数をまとめると…
Local:非 hybrid 型Disp:分散力補正あり下線:長距離補正あり
いくつかの代表的な汎関数
基本的な GGA 汎関数
- BLYP (Becke-Lee-Yang-Parr)
- PBE(Perdew-Burke-Ernzerhof)
meta GGA 汎関数
- BMK(Boese-Martin functional for Kinetics)
- ミネソタシリーズ(M06 など)
Hartree-Fock 交換項と組み合わせた hybrid 型の汎関数
- B3LYP
- 以前は実質上の業界標準(デファクトスタンダード)であるかのように多用
- 長距離電子相関の見積もりが不得意であることが知られるようになった
- 長距離補正を含む「CAM-B3LYP」、分散力補正を含む「B3LYP-D3」などが開発されている
- PBE0
- PBEPBE
長距離補正を含む汎関数
- CAM-B3LYP
- ωB97シリーズ(ωB97, ωB97-X, ωB97-XD)
- LC-BOP
分散力補正を含む汎関数
- B3LYP-D3
- ωB97X-D
- ミネソタシリーズ(M06-2X, X11 など)
hybrid 交換・相関汎関数 📊
- hybrid 型は、LSDA / GGA / mGGA などの交換汎関数に対して、一定の割合で Hartree-Fock 交換積分 $E_\mathrm{x}^\mathrm{HF}$ を混合した汎関数です。
- 非 hybrid 型(local 型)と hybrid 型の汎関数ペア(例:BLYP vs B3LYP)について、計算される物性値の平均二乗偏差(RMSD)を比較してみると…
NCD:分子間相互作用エネルギーID:異性化エネルギーBH:反応障壁の高さ
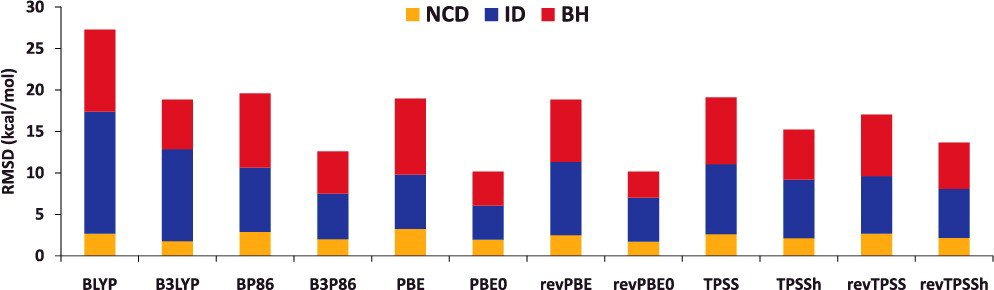
- $E_\mathrm{x}^\mathrm{HF}$ を適度に hybrid することで計算精度が向上
分散力補正 📊
- 標準的な DFT の弱点のひとつは、分散力(van der Waals 相互作用) の記述ができない
- このために、分子集合体における分子間相互作用を過小評価する傾向にある
- Grimme は、分子力場などで用いられるように経験的なパラメータを用いて、各原子対に対する引力的なエネルギー項を付加する分散力補正を提案
- Grimme の分散力補正のあり・なし(例:BLYP と BLYP-D2, BLYP-D3)について、計算される物性値の平均二乗偏差(RMSD)を比較してみると…
NCED:分子間相互作用エネルギーIE:異性化エネルギー
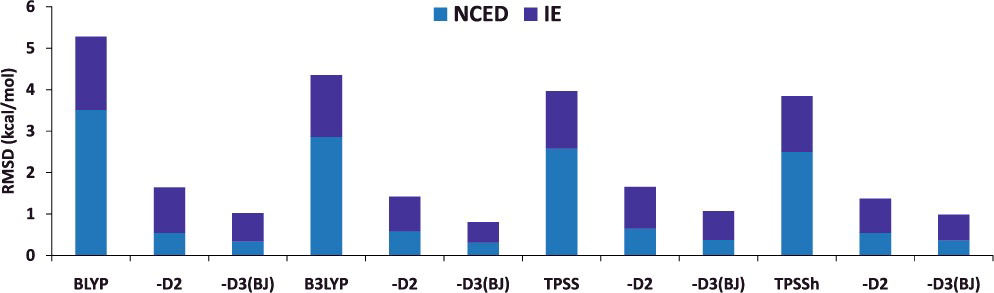
- Grimme の分散力補正を加えることで、コストを追加することなく、計算精度を向上させることができる
交換・相関汎関数のベンチマーク 📊
- 200 個の汎関数について、ベンチマーク計算をしてみると…
- 汎関数名の右にある数字は、計算精度のランキング
- 左にあるラベルは、評価した物性値:
NCED/NCED/NCD:分子間相互作用エネルギーIE/ID:異性化エネルギーTCE/TCD:熱化学量BH:反応障壁の高さ

- GGA から meta GGA に変えても、多くの場合、計算精度はそれほど良くはならない
- 非 hybrid 型(local 型)から hybrid 型に変えると、ほとんどの場合、計算精度が向上
🤠 力試し Quiz
密度汎関数理論(DFT)法に関する次の文章について、適切なものをすべて選んでください。
- DFT は、HF と同様に、波動関数を試行関数とする方法であり、その基礎となる Kohn-Sham 方程式は、シュレディンガー方程式を近似したものであると言える。
- DFT は、電子同士の相互作用に由来する「電子相関」について、Hartree-Fock 法と比較して、より定量的な精度で考慮することができる計算方法である。
- 一般的に、hybrid 型の汎関数は、非 hybrid 型の汎関数に比べて、様々な物性値を計算するときに、その精度が高いと期待できる。
- DFT の汎関数として代表的なものは B3LYP であり、この汎関数は長距離補正を含むので、分子集合体系の分子間相互作用などについても、定量的な精度で正しく評価できる。
量子化学計算の代表的な基底関数
Gaussian で利用できる様々な基底関数

基底関数とは?
- 任意の波動関数 $\Psi$ を有限個の既知の関数 $\phi_1, \phi_2, …, \phi_n$ の線形結合で表すという近似(線形近似)を考える $$ \Psi = c_1 \phi_1 + c_2 \phi_2 + … + c_n \phi_n = \sum_i^n c_i \phi_i $$
- この既知の関数 $\phi_1, \phi_2, …, \phi_n$ のことを基底関数 と呼ぶ
- 展開係数 $c_1, c_2, …, c_n$ の値を変えると、波動関数 $\Psi$ が変わる
展開係数とは?
- 量子化学計算では、あらかじめ適切にパラメータを設定した基底関数 ${\phi_n}$ を使って、展開係数 ${c_n}$ の値について、最適なものを探そうとする
- つまり、計算の途中で…
- 基底関数 ${\phi_n}$ は変えずに、
- 展開係数 ${c_n}$ の値だけを変える。

基底関数の選び方
- 基底関数には様々な種類があり、どのような分子を解析したいのか、何を調べたいと思っているのか、どのような計算方法を用いるのか、それぞれに応じて、適切に選択する必要がある
- 基底関数の個数が多いほど、電子分布を柔軟に表現できるので、計算精度が高くなる
- 計算精度が高くなればなるほど、計算コストも高くなってしまう
- 計算精度と計算コストのバランスを考えて、適切に選ぶ
🟩 水素分子の場合
- 水素分子を表す波動関数 $\Psi$ は、たとえば、2個の水素原子 $\mathrm{H}_a$ と $\mathrm{H}_b$ の中心に置いた1s 原子軌道 $\phi_a$ と $\phi_b$ の線形結合として、次のように表すことができる $$ \Psi = c_a , \phi_a + c_b , \phi_b $$
- 水素原子については、1s 軌道の厳密解が次のように分かっている $$ \psi_\mathrm{H1s} = \sqrt{\frac{1}{\pi}} \exp(-r) $$
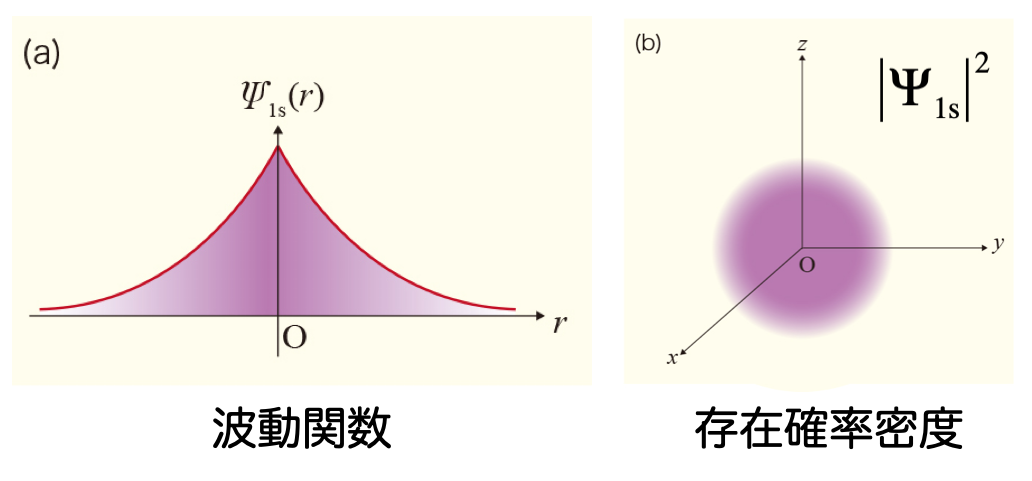
- したがって、水素原子の 1s 軌道を参考にして、$\exp(-\zeta r)$ 型の関数を基底関数として使っても良さそうだ
$$ \phi_a = \exp(-\zeta r) $$
- このような関数をスレーター型関数 と呼ぶ
- 係数 $\zeta$ は、関数の「広がりの程度」を表す変数
- 水素原子の厳密な解析解(= 電子の分布を適切に表すことができる)なので、計算精度は高い

- ただし、数値計算の計算効率は悪い
- 図にあるように、原子の中心($r = 0$)で値が不連続になるから、数値的に積分することが難しい
- 計算効率が悪いので、ふつうは、量子化学計算では使わない
🟩 ガウス型関数
- 量子化学計算では、スレーター型関数 $\exp(-\zeta r)$ の代わりに、$\exp(-\alpha r^2)$ 型の関数を基底関数として使う
$$ \phi_a = \exp(-\alpha r^2) $$
- このような関数を ガウス型関数 と呼ぶ
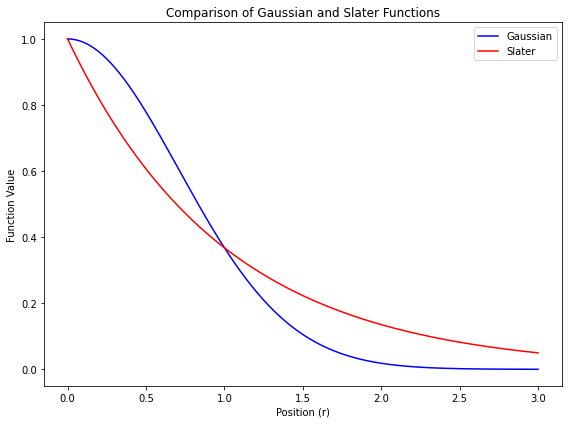
- 係数 $\alpha$ は、関数の「広がりの程度」を表す変数
- 量子化学計算の前に、あらかじめ設定されている定数(計算の途中で変化させない)
- ガウス型関数は、原子軌道に対する近似解なので、計算精度は高くはない
- ただし、数値計算の計算効率が良い
- 上の図にあるように、原子の中心($r = 0$)でも値が連続になるから、数値積分が簡単
- 計算精度の悪さは、拡がりの程度を変えたガウス型の基底関数をいくつか線形結合させることでカバーする
- いくつかのガウス型関数を線形結合させたものを# 短縮型ガウス基底とよぶ
- たとえば…
$$ \phi_\mathsf{blue} = c_\mathsf{cyan} \, \chi_\mathsf{cyan} + c_\mathsf{pink} \, \chi_\mathsf{pink} + c_\mathsf{green} \, \chi_\mathsf{green} $$ $$ = \left(1.33 \; e^{-0.59 \; r^2_\mathsf{cyan}}\right) + \left(-0.57 \; e^{-1.28 \; r^2_\mathsf{pink}}\right) + \left(0.04 \; e^{+0.06 \; r^2_\mathsf{green}}\right) $$
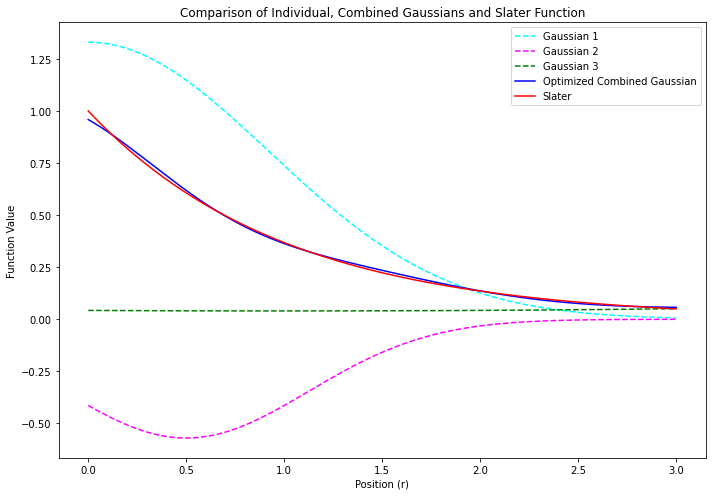
- 青い線で示す 短縮型ガウス関数 は、赤い線で示すスレーター型関数のかたちを、まあまあ良く再現している
基底関数の種類 1️⃣
最小基底系(STO-nG基底系)
- 例
STO-3G- 3種類のガウス型関数(
3G)を足し合わせて、スレーター型軌道(STO)に似せたもの
- 3種類のガウス型関数(
STO-4GSTO-5G
- 計算精度の比較
STO-3G<STO-4G<STO-5G
- 計算コストは低いが、計算精度も低いので、実験結果と比較するなどの実用的な解析に用いることはあまりない
基底関数の種類 2️⃣
Pople 系
- 例
3-21G/6-31G/6-311G
- 計算精度の比較
3-21G<6-31G<6-311G
- John A. Pople (1998年ノーベル化学賞受賞)らが提案した基底関数系
- 最小基底系に比べると、より柔軟に電子のふるまいを記述できるため、計算精度が改善される
- 原子価軌道に対して、拡がりの異なる複数の関数を組み合わせて表現する
- 一般的な有機化合物に対しては、基盤となる 6-31G に 分極関数 を加えた 6-31G(d) や 6-31G(d,p) などが、計算効率が良い・実用的な精度をもつ基底関数としてよく用いられている
🟩 分割価電子(split valence)基底関数
- 内殻軌道には1つ、価電子軌道には複数の短縮ガウス型関数を用いた基底関数系
- Pople 系の場合
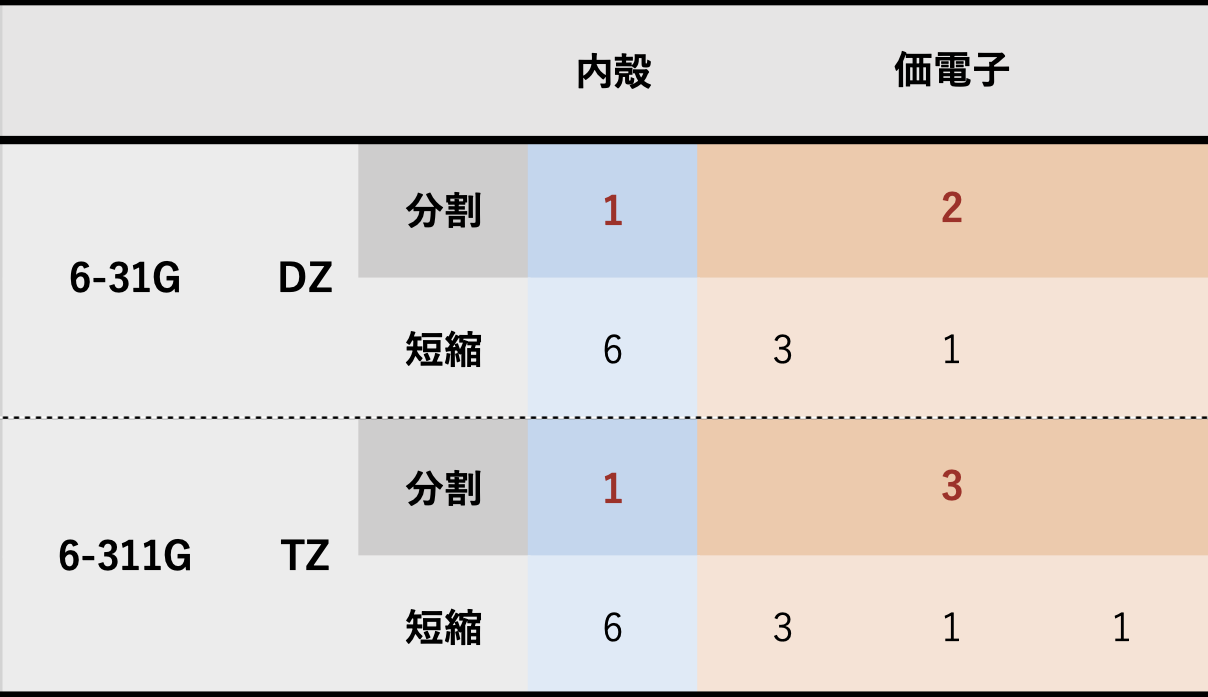
🟩 6-31G の場合
- 1つの占有軌道に対して…
- 内殻軌道
- 6個のガウス型を足し合わせた(短縮した)1種類の関数で記述
- 価電子軌道
- 3個のガウス型を短縮したもの+別の1個のガウス型を組み合わせて、計2種類の関数で記述
- 2種類の関数で原子価軌道を表すものを double zeta (DZ) 型とよぶ
- 内殻軌道
🟩 6-311G の場合
- 1つの占有軌道に対して…
- 内殻軌道
- 6個のガウス型を足し合わせた(短縮した)1種類の関数で記述
- 価電子軌道
- 3個のガウス型を短縮したもの+別の1個のガウス型+別の1個のガウス型を組み合わせて、計3種類の関数で記述
- 3種類の関数で価電子軌道を表すものをtriple zeta (TZ) 型とよぶ
- 内殻軌道
🟩 具体例

基底関数の種類 3️⃣
高精度計算に適した基底関数(Correlation-Consistent 基底系)
- 電子相関を取り込んだ高精度計算に適した基底関数として Thom H. Dunning, Jr. らの cc-pVnZ 基底関数(n = D, T, Q, 5, 6)がある
- 計算精度の比較
cc-pVDZ<cc-pVTZ<cc-pVQZ
- 応用研究の中では、double zeta 精度の cc-pVDZ が頻繁に用いられる
- double zeta 精度では、電子相関効果の取り込みが不十分である場合もある
- 化学反応などにおいて 10 kcal/mol 程度のエネルギー差を定量的に議論したいときには、cc-pVTZ 程度(triple zeta 精度)の基底関数を CCSD(T) レベルの計算手法と組み合わせて用いる
- double zeta 精度では、電子相関効果の取り込みが不十分である場合もある
分極関数とは?
- 分子の複雑な構造を適切に記述したい場合には、各原子上に配置した基底関数に 分極関数(polarization function) を追加することで、電子分布が柔軟に変形する自由度を与えることができる
分極関数(d 型関数)
- p 軌道をもつ水素以外の原子に対しては、d 型の関数を追加する
分極関数(p 型関数)
- 球対称な s 軌道のみを持つ水素原子に対しては、p 型の関数を追加する
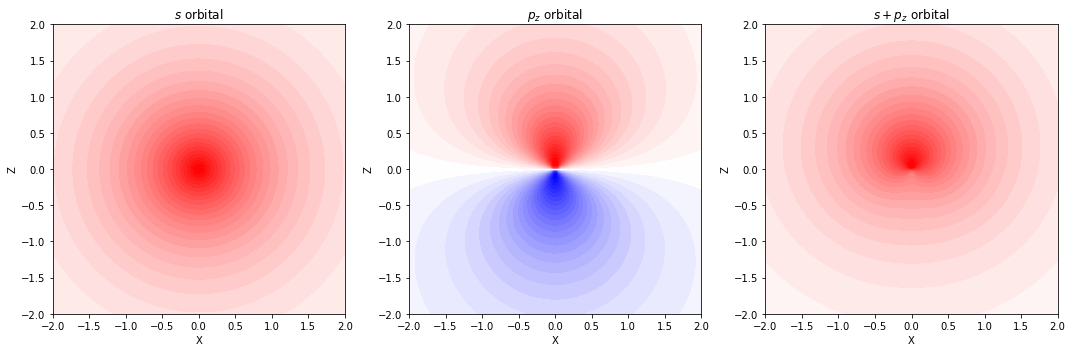
表記方法 / 指定方法 🔤
- Pople 系に対して、分子内にある水素以外の原子に分極関数を追加する場合
3-21G(d)or3-21G*6-31G(d)or6-31G*
- Pople 系に対して、水素以外の原子に分極関数を追加した上で、水素原子にも分極関数を追加する場合
3-21G(d,p)or3-21G**6-31G(d,p)or6-31G**
- cc-pVnZ 基底関数(n = D, T, Q, 5, 6)は、水素原子および水素以外の原子のどちらにも、全ての原子に分極関数が追加される
Gaussian で分極関数を追加するには

分散関数とは?
- 負電荷を帯びた分子は、中性分子と比較して、電子分布が広がっている場合がある
- このような場合、物性諸量を正しく見積もるためには、電子分布の広がりを記述するために 分散関数(diffuse function) を加えることができる
表記方法 / 指定方法 🔤
- Pople 系に対して、分子内にある水素以外の原子に分散関数を追加する場合
3-21+G(d)or3-21+G*6-31+G(d)or6-31+G*
- Pople 系に対して、水素以外の原子に分散関数を追加した上で、水素原子にも分散関数を追加する場合
3-21++G(d,p)6-31++(d,p)
- cc-pVnZ 基底関数(n = D, T, Q, 5, 6)に対して、水素原子および水素以外の原子のどちらにも、全ての原子に分散関数を追加する場合
aug-cc-pVDZaug-cc-pVTZ
Gaussian で分散関数を追加するには

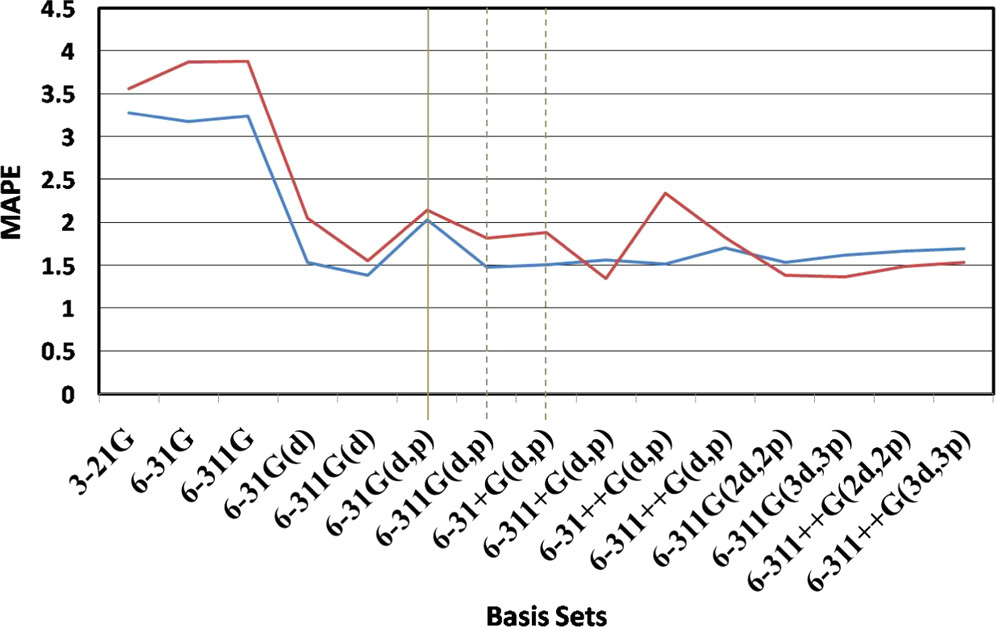
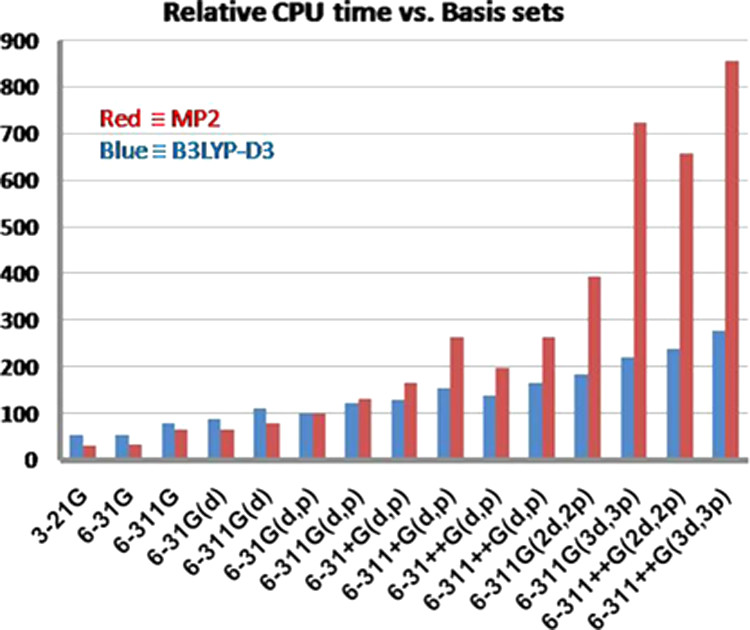
基底関数のベンチマーク(VSCF-PT2 計算の場合) 📊
🟩 基底関数と計算時間(VSCF-PT2 計算の場合) 📊
オススメの計算手法と基底関数は?
- 一般的な有機化合物の基底状態の物性を調べようとする場合、まずは B3LYP/6-31G(d) や B3LYP/6-31G(d,p) を使うことが多いです
- 原子間の結合距離を定量的に議論するには、最低でも double zeta 精度(
6-31G)が必要 - 原子間の結合角度を定量的に議論するには、分極関数(
6-31G(d))が必要
- 原子間の結合距離を定量的に議論するには、最低でも double zeta 精度(
🟩 DFT 汎関数と基底関数の組み合わせ
計算条件の表し方
基本的な表記方法 🔤
- 量子化学計算の計算精度や計算コストは、主に、計算方法と基底関数の組み合わせで決まる
- 計算方法の種類 と 基底関数の種類 を スラッシュ(
/) で挟んで表記することが多い - たとえば…
B3LYP/6-31G(d)MP2/cc-pVDZ
少し複雑な表記方法 🔤
- あるレベルで 構造最適化 した後、より高精度なレベルで エネルギー計算 をおこなった場合、2つの計算レベルを ダブルスラッシュ(
//) で挟んで表記することがある - たとえば…
CCSD(T)/aug-cc-pVTZ//B3LYP/6-31G(d)- 最初に、手軽に電子相関の寄与を考慮できる密度汎関数法(
B3LYP汎関数)と小さな基底関数(6-31G(d))の組み合わせで、構造最適化を実行 - 次に、
B3LYP/6-31G(d)レベルで最適化した分子構造を用いて、高精度な量子化学計算手法(CCSD(T))と大きな基底関数(aug-cc-pVTZ)の組み合わせで、エネルギー計算を実行
- 最初に、手軽に電子相関の寄与を考慮できる密度汎関数法(
🤔 金属化合物の場合の注意点は?
- 金属を含む系の場合、「電子の数が多い」、特に「内殻電子が多い」ことが原因で、6-31G などでは不十分だったり、コストが高くなってしまうことがあります
- このような場合、「内殻電子を近似する」ことで、適切に扱うことができる場合が多いです
- 具体的には…
- 内殻電子を「有効内殻ポテンシャル(effective core potential; ECP)」
- LanL2DZ
🤔 水素原子にも分散関数を追加した方がいい場合とは?
- 分子同士が水素結合した錯体を扱う場合、6-31G(d,p)などが良いかと思います
🤠 力試し Quiz
基底関数に関する次の文章について、適切なものをすべて選んでください。
- 最小基底系のひとつである STO-3G は、計算コストは低いが、計算精度は低いので、実験結果との定量的な比較などの実用的な解析に用いることは難しい。
- Pople 系基底関数のひとつである 6-311G は、一般に、同じ Pople 系基底関数である 3-21G よりも柔軟に電子のふるまいを記述できるため、計算精度が高い。
- Pople 系基底関数のひとつである 6-31G などは、固体表面や結晶などの周期性をもつ分子系の電子状態を解析しようとするときに使うことはあまりない。
- 水素分子($\mathrm{H_2}$)についての量子化学計算をおこなう場合、基底関数として 6-31G と 6-31+G(d) のどちらを使っても、全エネルギーなどの計算結果は、まったく同じになる。
- フラーレン($\mathrm{C_{60}}$)についての量子化学計算をおこなう場合、基底関数として 6-31+G(d) と 6-31++G(d,p) のどちらを使っても、全エネルギーなどの計算結果は、まったく同じになる。
- 基底関数には様々な種類があるが、どのような場合でも、量子化学計算プログラムで用いることができる「最も高い精度の基底関数」を選べば良い。
- 負電荷を帯びた分子は、中性分子と比較して電子分布が広がっているので、電子分布の広がりを記述するために、基底関数には 6-31G ではなく、分極関数を加えた 6-31G(d) を用いた方がよい。
☕ 休憩 14:15 〜 14:30
🧑🏫 講義③ 14:30 〜 16:00
量子化学計算に基づく構造最適化
💻 実演:Gaussian を用いた水分子の安定構造の探索
- 最適化される様子を確かめるため、HOH 結合角を 150° 程度にしたものを初期構造とした
分子の安定構造の探索
- 各原子核に働く力(エネルギー勾配 $\frac{\partial E}{\partial Q}$)の方向にカタチをちょっとずつ変化($x_\mathrm{new} = x_\mathrm{old} - \alpha \frac{\partial E}{\partial Q}$)させることで、分子はより安定となる( = エネルギーが小さくなる)
- $E(x_\mathrm{new}) < E(x_\mathrm{old})$

- 「カタチをちょっとずつ変化させる」を繰り返すことで、分子の立体構造を半自動的に最適化できる
- 実際には、多くの量子化学計算プログラムは、エネルギー勾配の方向に動かすという単純な方法(勾配降下法)ではなく、もっと効率的なアルゴリズムを使っている
- Gaussian では、デフォルトでは、GEDIISというアルゴリズムを用いる
- 実際には、多くの量子化学計算プログラムは、エネルギー勾配の方向に動かすという単純な方法(勾配降下法)ではなく、もっと効率的なアルゴリズムを使っている
計算例:水分子の構造最適化

量子化学計算に基づく振動解析
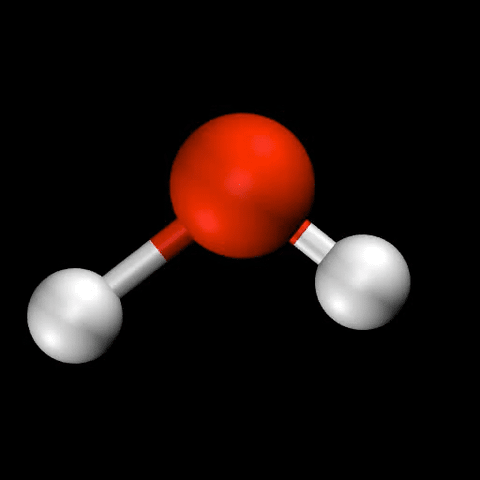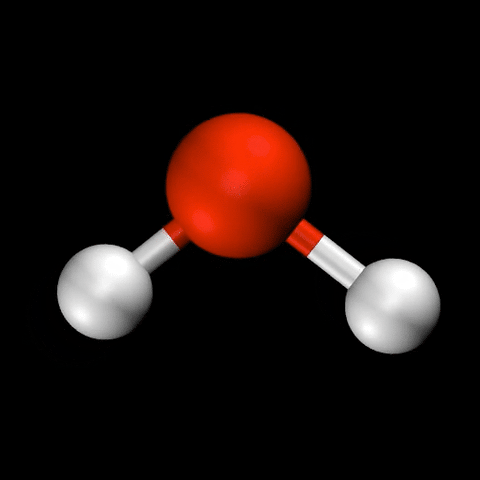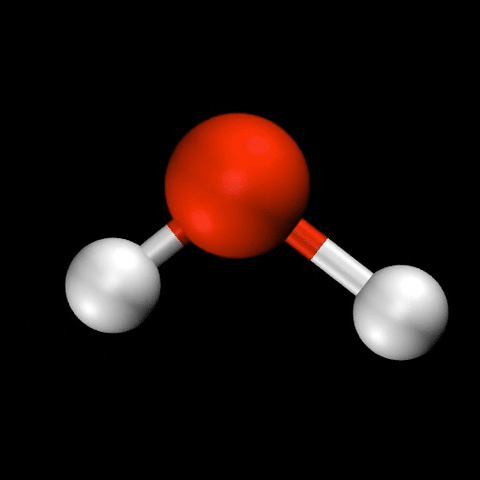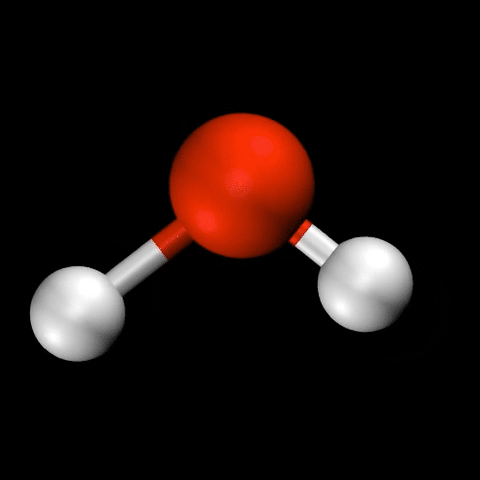
分子振動とは?
- 水($\mathrm{H_2O}$)の変角振動 / 対称伸縮振動 / 逆対称伸縮振動
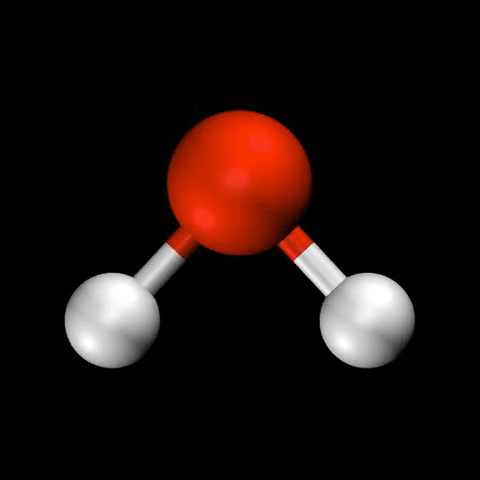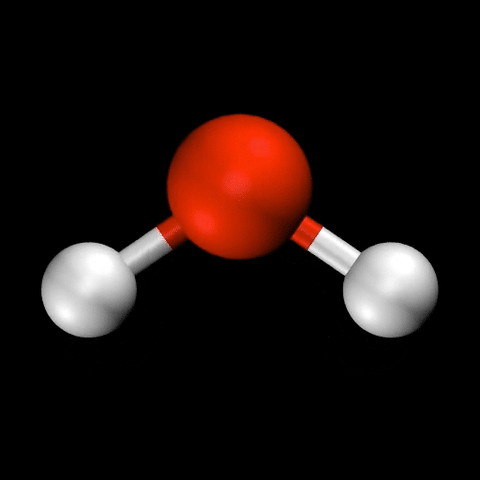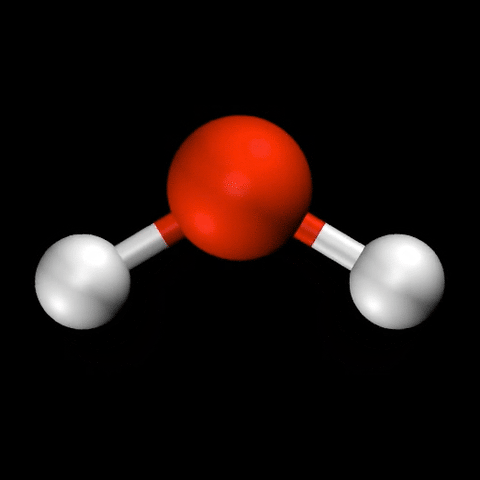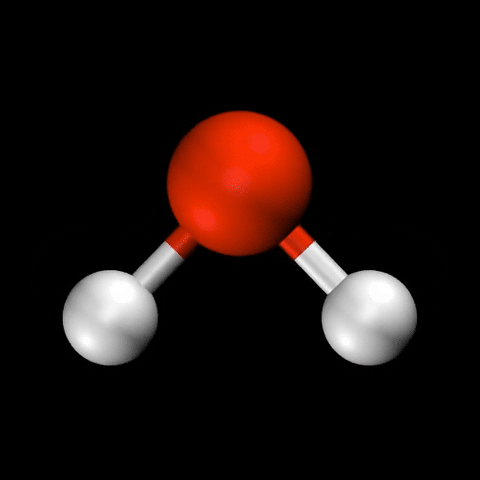
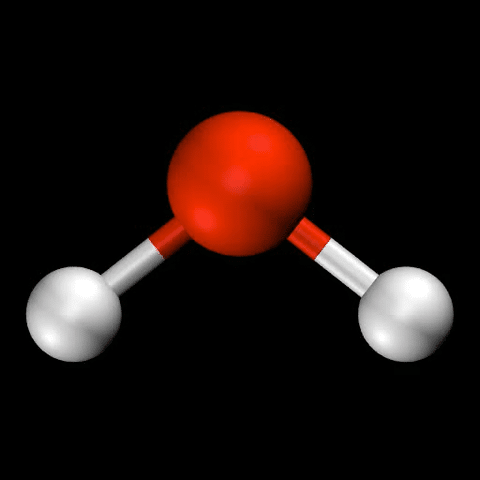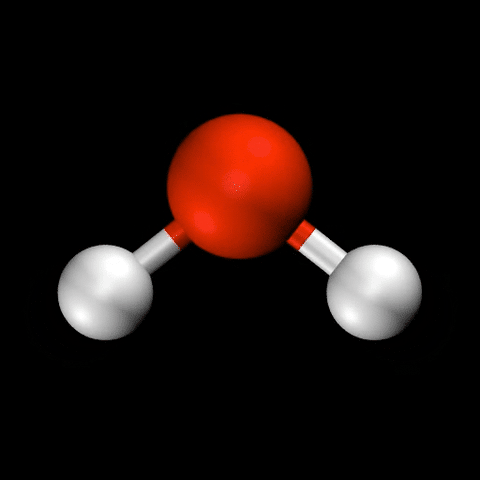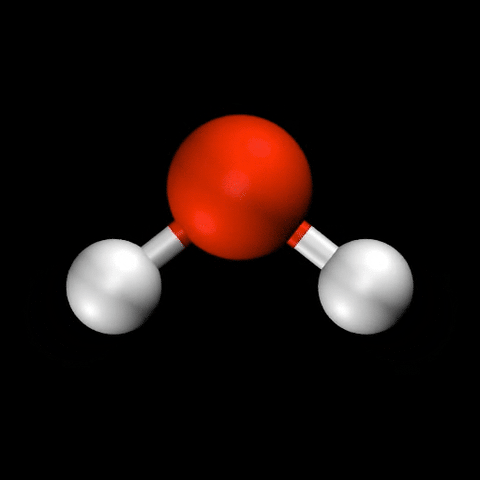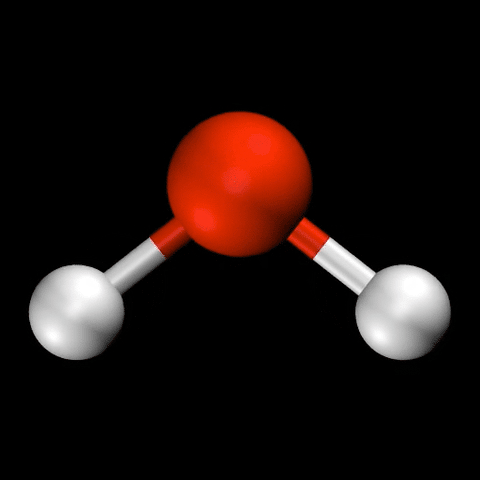
🤔 化合物の反応性について、熱や光など、化合物の特性以外の要因の影響は見ることは?
- 「熱」については、量子化学計算では「振動解析」で得られる情報を元にして、近似的に、その影響を調べます
- 具体的には、分子が振動する状態を理論的に解析して、外部から「熱」が与えられたときに、分子がどのようにそのエネルギーを振動運動に変えることができるかを予測します
- 化学反応に伴う自由エネルギー変化など、熱力学的な性質について、近似的にですが、見積もることができます
振動解析とは?
- 分子固有の振動数と赤外強度を理論的に計算する方法
- 実験的に測定された赤外スペクトルの解釈を補助する手段として活用されている
- 各振動モードに対するラマン強度を計算することも可能
- 振動状態に基づいて、分子の熱力学的な情報(自由エネルギーなど)を計算することが可能
- ➡ 振動状態を解析しないと、ある温度における自由エネルギーの大きさなど、分子の熱力学的な性質についての詳しい情報が得られない
- 最適化した構造が「安定点」か「不安定点(遷移状態)」かを見分けることにも使える
赤外吸収スペクトル 📈 とは?
振動解析の計算手順
- 対象とする分子について、構造最適化を実行(安定構造を探索)する
- 構造最適化を実行したときと同じ量子化学計算レベルで、振動解析を実行する
💻 実演:Gaussian を用いた水分子の振動解析
計算例:水分子の振動解析

🟩 振動解析に基づいた熱力学量の見積もり
- 分子の振動状態に基づいて、電子状態のエネルギーに対して、 熱力学量を「近似的に」算出するための補正をおこなうことができる
- 振動数が低い振動モードほど、熱力学補正に対する寄与が大きい
- 「近似」なので、大きく構造が揺らぐ柔軟な分子については、誤差が大きくなる場合がある
- 求めることができるのは…
- ゼロ点エネルギー(Zero Point Energy, ZPE)振動補正 $$ E_0 = E + \mathrm{ZPE} $$
- 熱力学補正 $$ E_\mathsf{total} = E_0 + E_\mathsf{並進} + E_\mathsf{回転} + E_\mathsf{振動} $$
- エンタルピー補正 $$ H = E_\mathsf{total} + k_\mathrm{B} T $$
- Gibbs 自由エネルギー補正
$$
G = H - T S_\mathsf{total}
$$
- $S_\mathsf{total} = S_\mathsf{並進} + S_\mathsf{回転} + S_\mathsf{振動} + S_\mathsf{電子}$
🟩 Gaussian で熱力学量を調べる

🟩 熱力学補正の具体例
- $\mathsf{C_2H_5 + H_2 \rightarrow C_2H_6 + H}$
- エネルギー変化(熱力学補正をしない場合)
- $\Delta E = E_\mathsf{生成物} - E_\mathsf{反応物}$ = 4.86 kcal/mol
- 反応エンタルピー
- $\Delta_r H^\circ(298\mathsf{K}) = H_\mathsf{生成物} - H_\mathsf{反応物}$ = 8.08 kcal/mol
- Gibbs 自由エネルギー変化
- $\Delta_r G^\circ(298\mathsf{K}) = G_\mathsf{生成物} - G_\mathsf{反応物}$ = 11.18 kcal/mol
分子振動の非調和性
- 高い精度(MP2/cc-pVTZ)で計算した場合

- MP2摂動法を用いることで、実験値にかなり近くなる
- 高波数の振動モード(対称伸縮&逆対称伸縮)では、誤差が大きい
- 分子振動を 調和振動子 だと見なす近似(調和近似)による誤差(非調和性)の影響だと考えられる
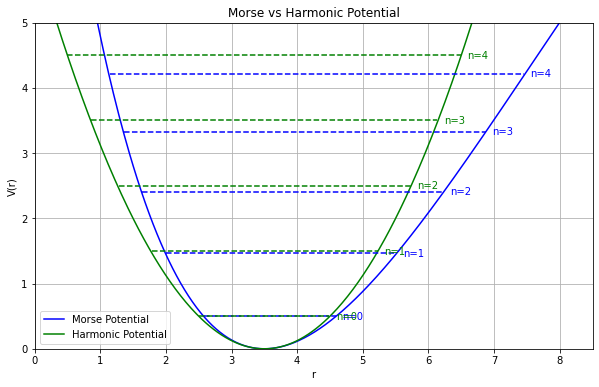
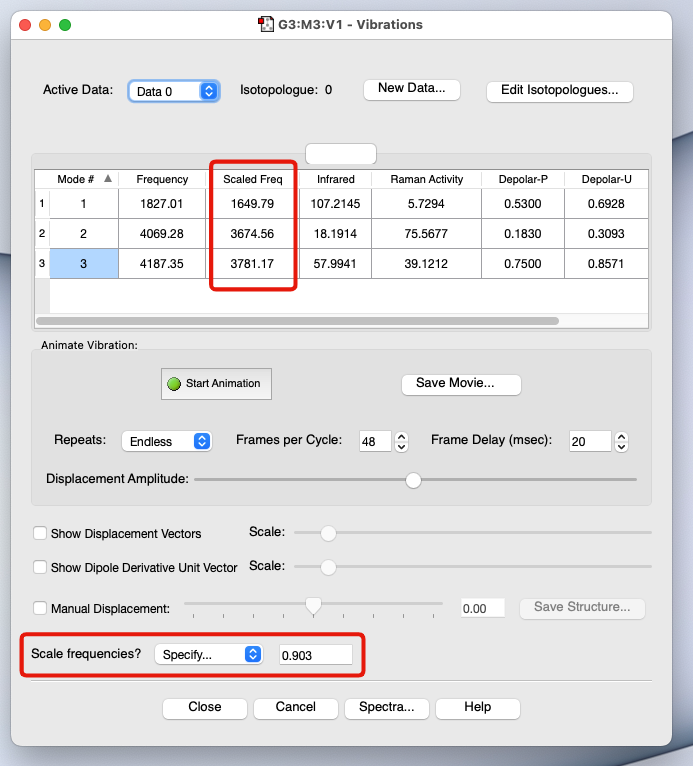
スケーリング因子
- 非調和性の問題を手軽に解決する場合には、振動数に適当な数字(スケーリング因子)を掛けて補正する
- 参考: https://cccbdb.nist.gov/vibscalejust.asp
- 事例:
HF/6-31G(d)の場合 → 0.903B3LYP/6-31G(d,p)の場合 → 0.961
🟩 非調和振動数解析
- 分子振動をより定量的精度で解析したい場合には、調和近似を越えた取り扱いが必要
- GAMESS では、非調和性を考慮した振動解析として、Vibrational SCF (VSCF) 法を利用することができる
- 詳細は こちら
- VSCF法で計算した場合

🤔 製剤などでの試験方法への応用は?
- 以前、振動分光に基づく結晶多形の解析について、ご相談をお受けしたことがあります
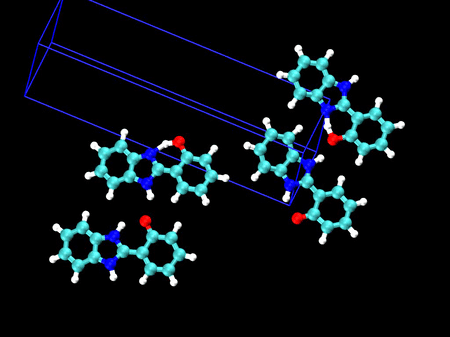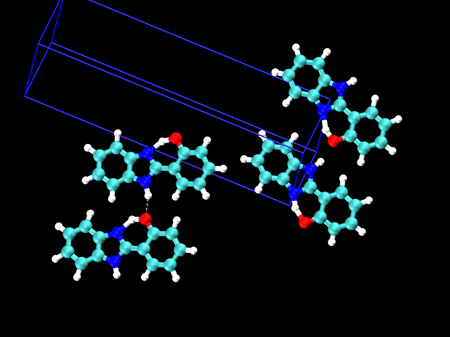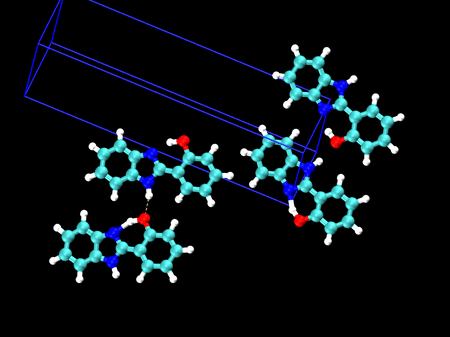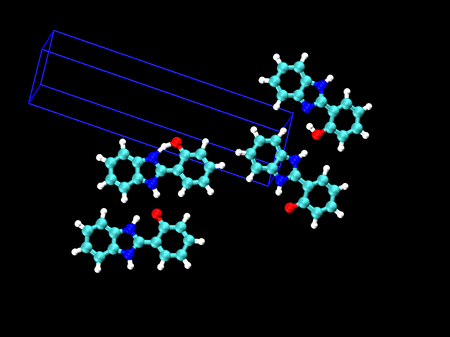
🎈 応用事例: 結晶多形を振動スペクトルで見分ける
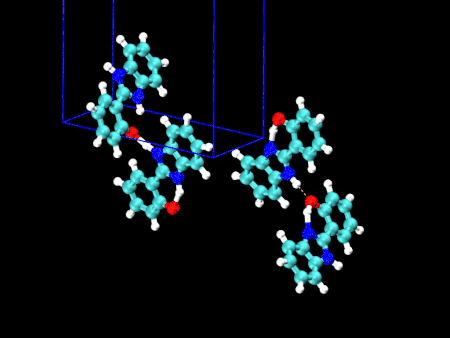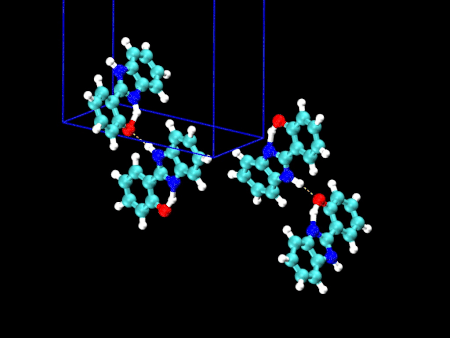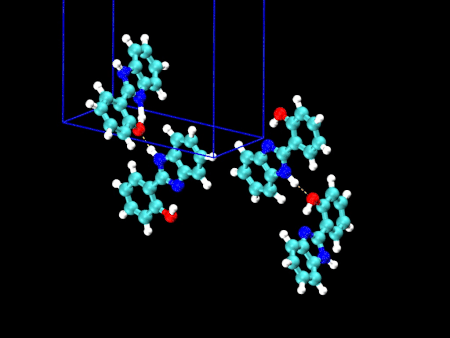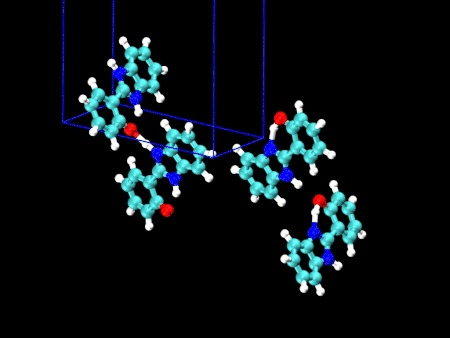
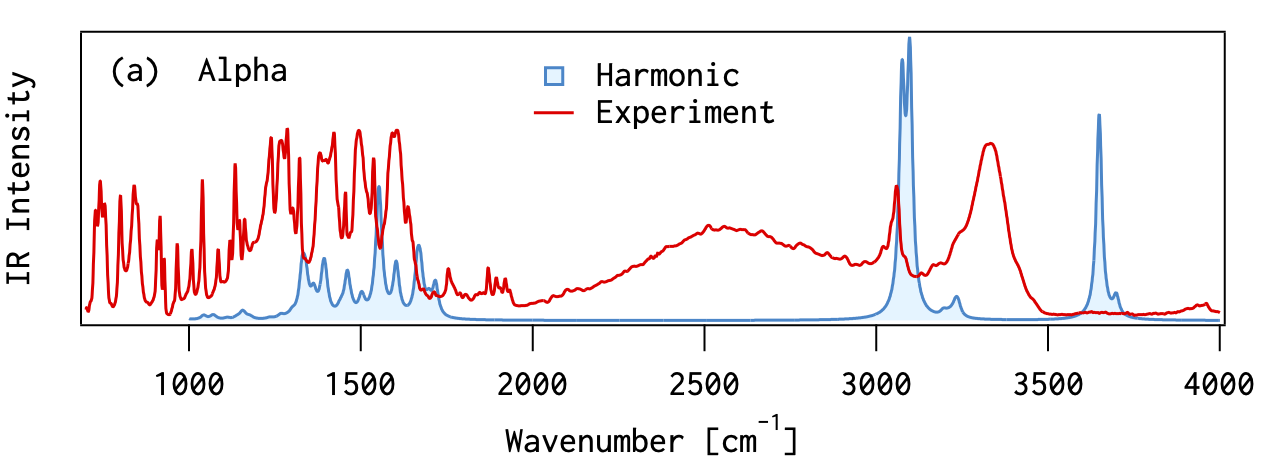
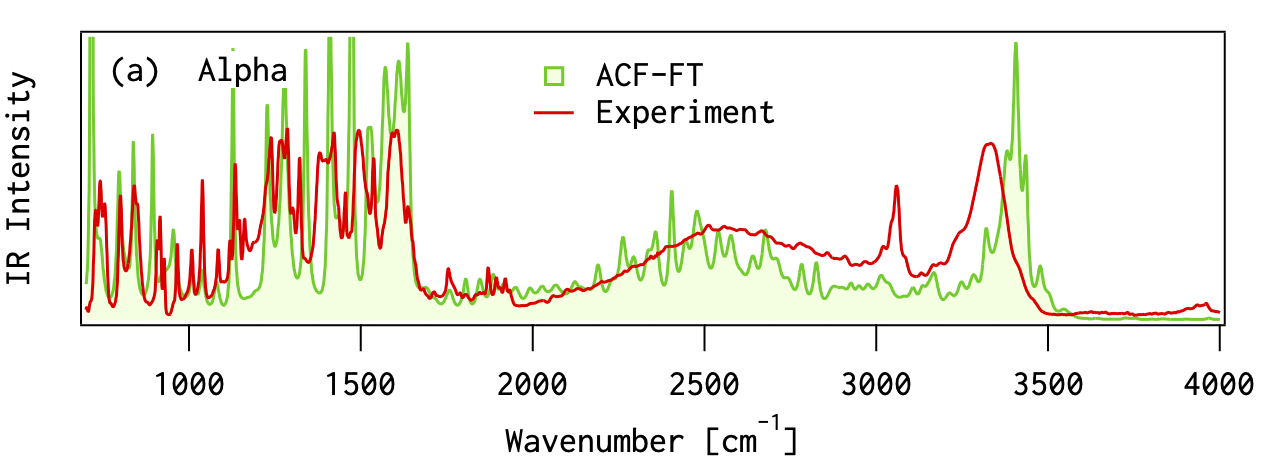
- HPBI という分子の結晶多形(左:α型 / 右:β型)
- 分子内の水素結合のある・なしで、3000〜3500 cm-1 のバンド形状が大きく異なることが分かりました


量子化学計算に基づく化学反応の解析
🎈 応用事例: 食品成分(リコピン 🍅)の異性化を促進したい


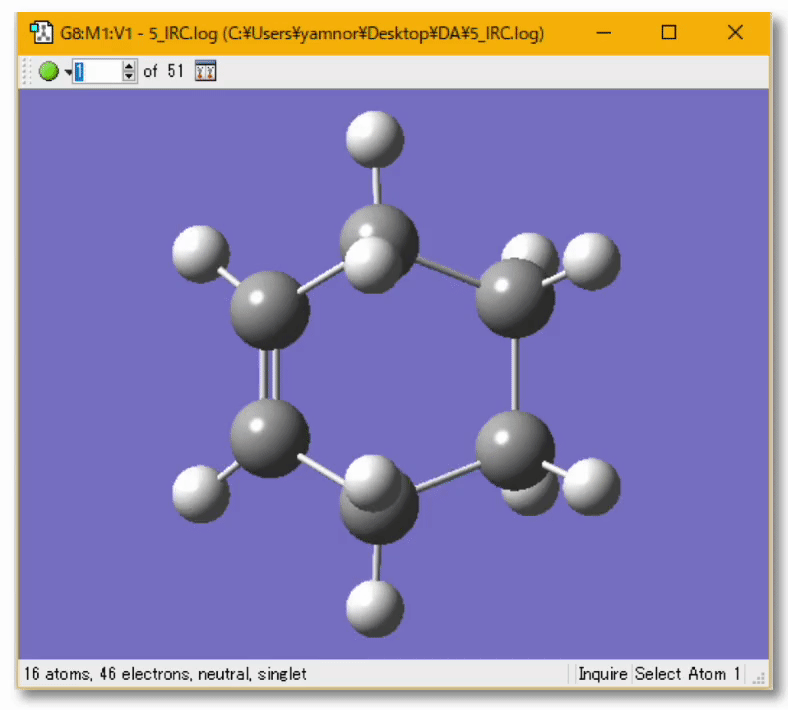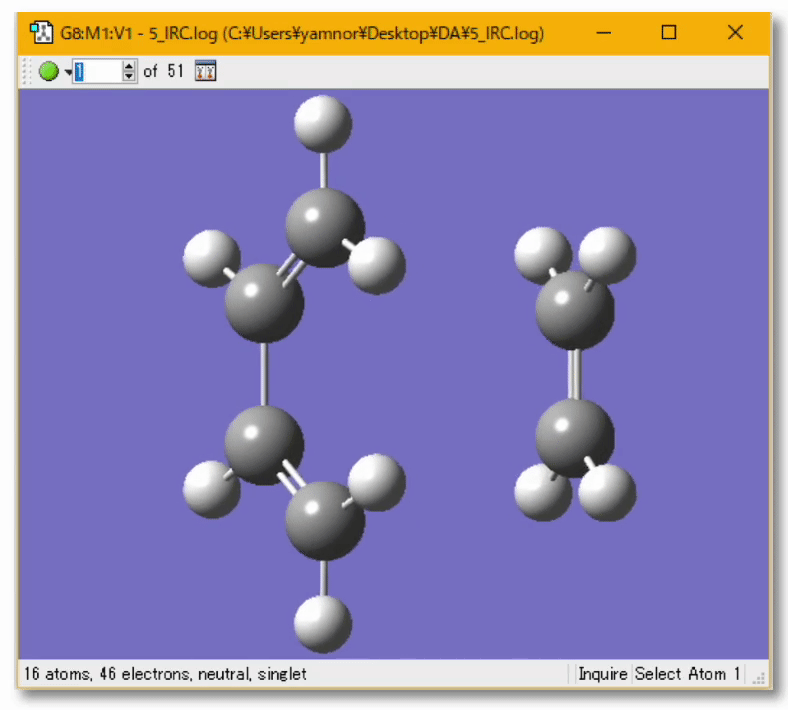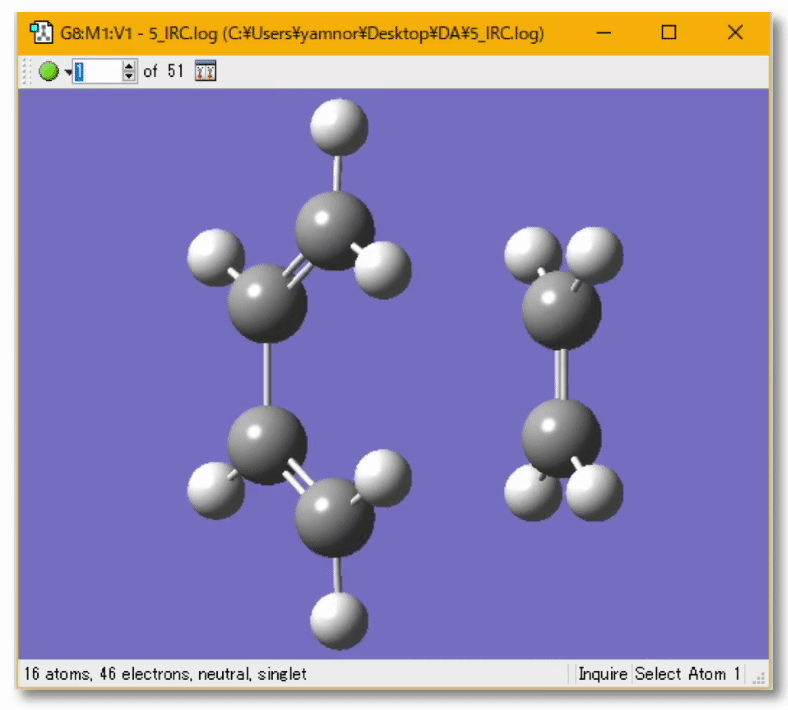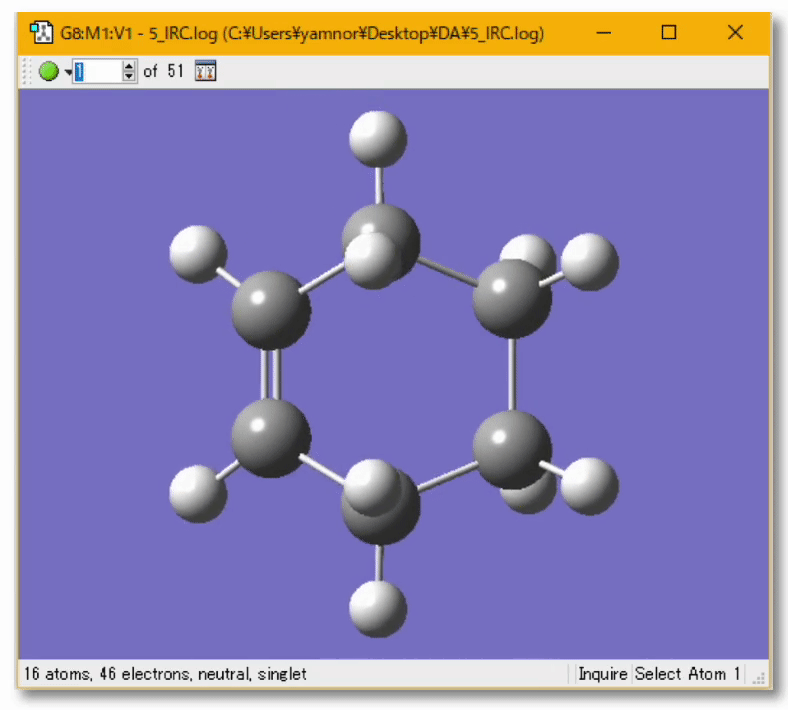
💻 実演:Gaussian を用いた Diels-Alder 反応の解析
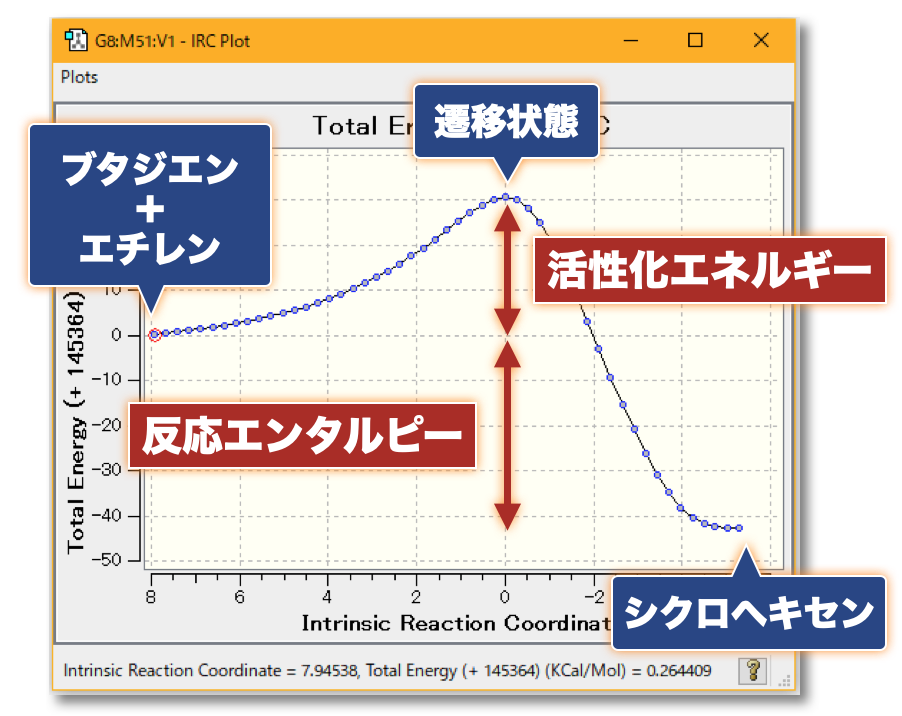
🤔 量子化学計算によって実験結果の予測、実験の手助けとなる計算を行うことは?
- 化学反応にともなう活性化エネルギー(反応障壁の大きさ)を見積もることで、「反応の速度」(反応速度定数)を理論的に見積もることができます
- 反応速度定数の見積もりには、「アレニウス則」や「遷移状態理論」などを用います
- また、反応物と生成物のエネルギー差(反応エンタルピー)から、ある温度における「反応物と生成物の分布比」を理論的に見積もることができます
- 分布比は「ボルツマン分布」に従います
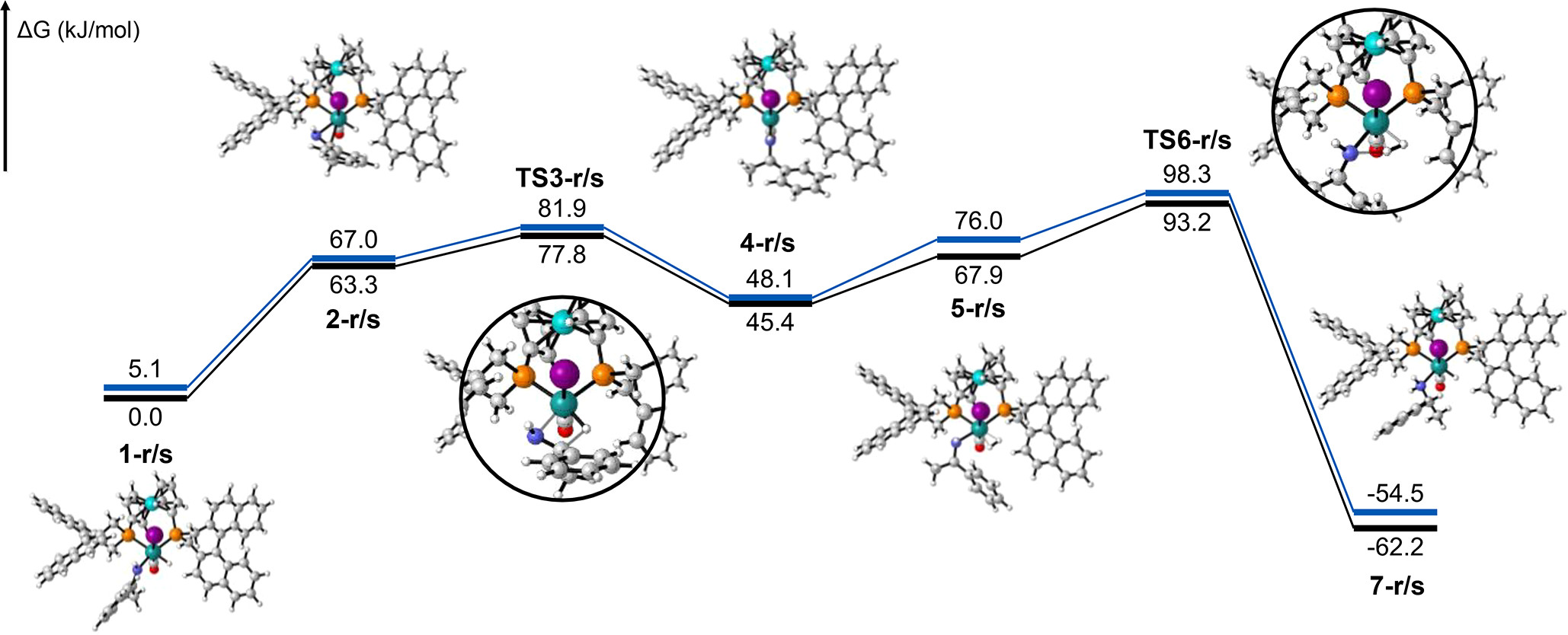
分子の遷移状態
- ある化学反応について、反応速度を議論するときには、その反応に伴う 遷移状態(Transition State; TS) を調べる必要がある
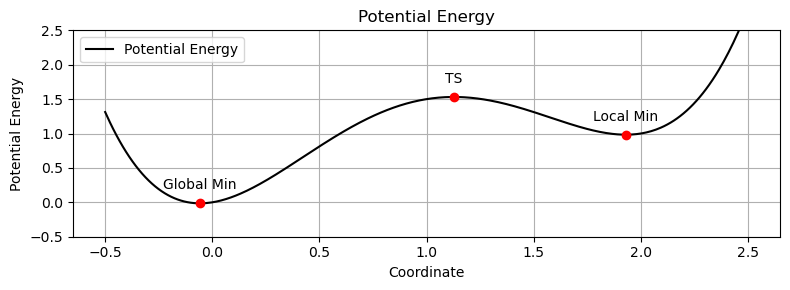
- たとえば、ある反応の速度定数 $k$ について、始状態と遷移状態とのエネルギー差、つまり、活性化エネルギー $\Delta G^{\ddagger}$ が分かっていれば、Eyring-Polanyi 式から…
$$ k = \chi \frac{k_\mathrm{B}T}{h}\exp\left(-\frac{\Delta G^{\ddagger}}{RT}\right) $$- $\chi$:遷移状態において、反応座標に沿った分子振動が一往復したときに反応する確率(透過係数)
- $h$: プランク定数
遷移状態に基づく解析の具体例
- $\mathsf{FH + Cl \rightarrow F + H Cl}$
- 水素($\mathsf{H}$)の場合
- $\Delta G^{\ddagger}$ = 17.26 kcal/mol
- $k(298\mathsf{K}) = \frac{k_\mathrm{B}T}{h}\exp\left(-\frac{\Delta G^{\ddagger}}{RT}\right)$ = 1.38 $\mathsf{s}^{-1}$
- 透過係数 $\chi$ は 1 として計算
- 重水素($\mathsf{D}$) に置換した場合
- $\Delta G^{\ddagger}$= 18.86 kcal/mol
- $k(298\mathsf{K})$ = 0.0928 $\mathsf{s}^{-1}$
- ➡ 重くなることで、反応速度が遅くなる
- 水素($\mathsf{H}$)の場合
🎈 応用事例: 色素材料の円偏向性を制御したい


🎈 応用事例: 酵素反応のメカニズムを解析したい
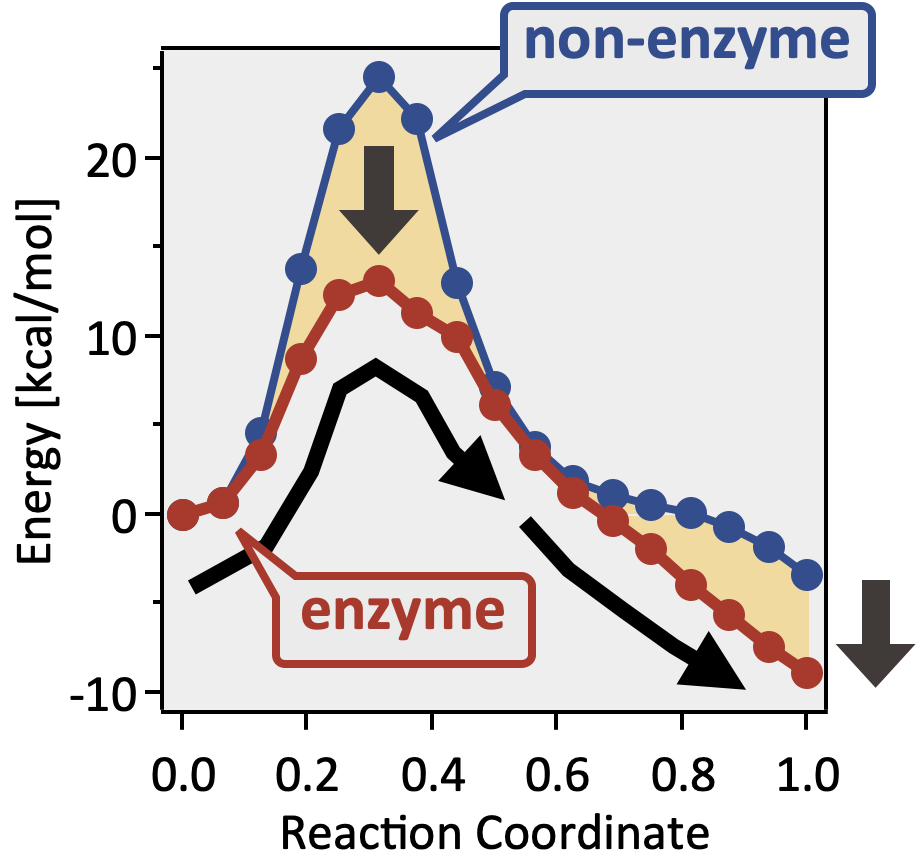
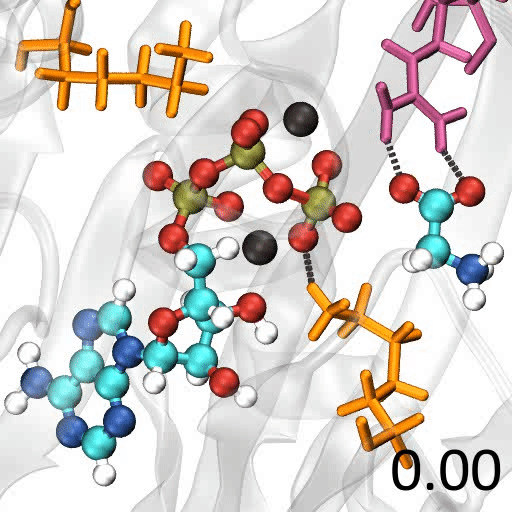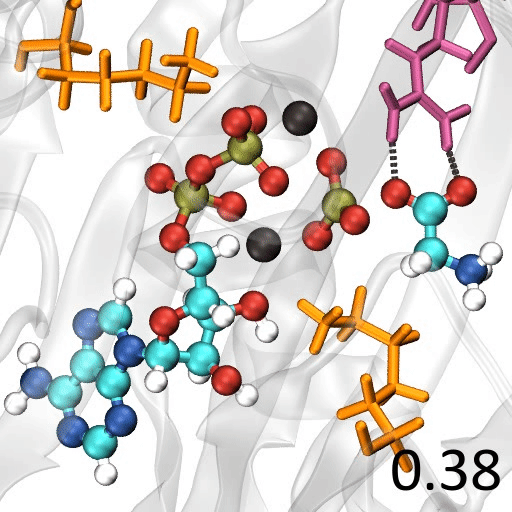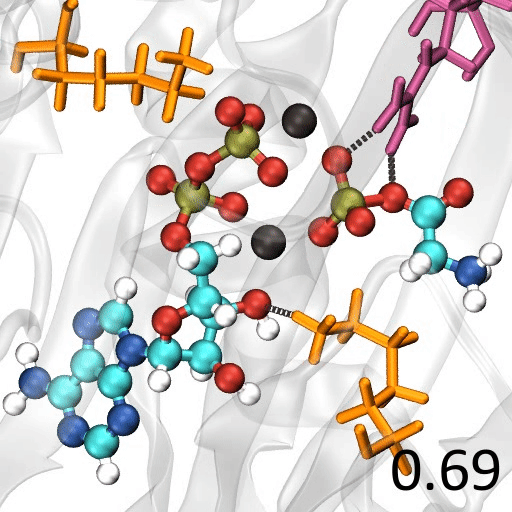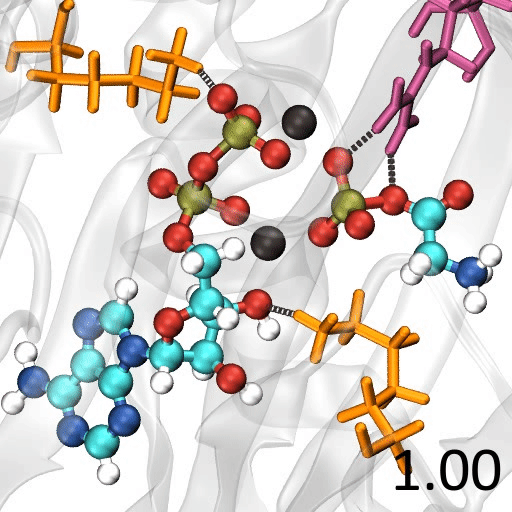
遷移状態の探索
- 多くの量子化学計算プログラムには、遷移状態を探索する機能が備わっている
- 単純に「構造最適化の逆」($x_\mathrm{new} = x_\mathrm{old} + \alpha \frac{\partial E}{\partial Q}$)をやっても、うまくいかない

- エネルギーの二次微分($\frac{\partial^2 E}{\partial Q^2}$)を要素にもつ Hessian 行列 の固有値(力の定数 or 曲率:$\chi$)を求めて…
- Hessian 行列の負の固有値を持つ固有ベクトルの方向に少しずつ動かすという方法がある
- → Eigenvector Following 法
- 調和近似($E = \kappa Q^2$)からの歪みが大きな方向に少しずつ動かすという方法がある
- → 超球面探索法(参考: GRRMプログラム )
- Hessian 行列を計算するためのコストがまあまあ大きい
- ➡ 構造最適化よりも計算コスト(時間)がかかる
- Hessian 行列の負の固有値を持つ固有ベクトルの方向に少しずつ動かすという方法がある
🤔 反応の場などの前提条件は、事前に設定したうえで遷移状態を探索するのでしょうか?
- あらかじめ、「遷移状態に近いのはどのような構造か?」について、大まかな知識や前提が必要となります
💻 実演:Gaussian を用いたブタジエンの cis/trans 異性化反応の解析
- 遷移状態に近い(と予想される)構造から出発する
- 今回の場合、C-C 軸周りの回転角度を 90度くらいにしてみる
- 見つけようとしている遷移状態は捻れ型だと考えられるから
- 今回の場合、C-C 軸周りの回転角度を 90度くらいにしてみる
- 遷移状態探索の設定方法
Job Type
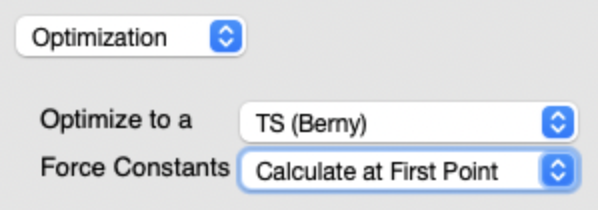
Optimizationを選択Optimize to aTS (Berry)Force ConstantsCalculate at First Point
化学反応のエネルギーダイアグラムを描く

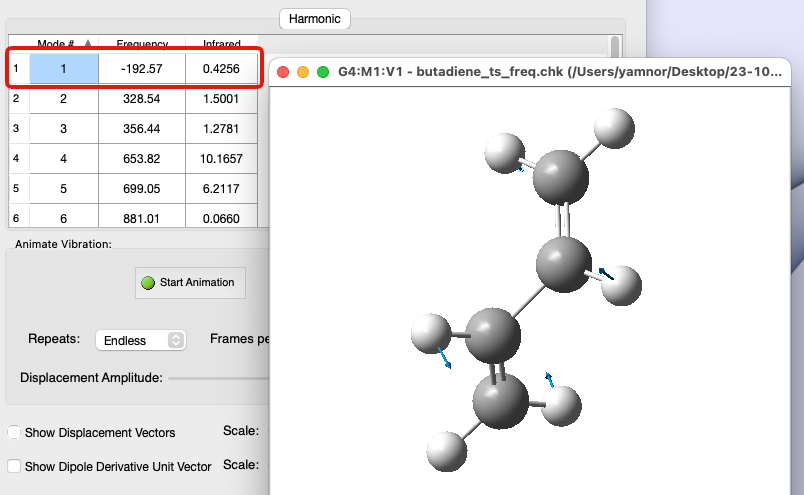
🟩 遷移状態で振動解析すると…
- 値が負(虚数)となる振動数がある
🟩 安定構造では…
- エネルギーの座標に関する一次微分(エネルギー勾配)が常にゼロである $$ \frac{\partial E}{\partial Q} = 0 $$
- 局所 安定状態(下に凸の放物線) であり、エネルギーの座標に関する二次微分の値が常に正 である $$ \frac{\partial^2 E}{\partial Q^2} > 0 $$

🟩 遷移状態では…
- エネルギーの座標に関する一次微分(エネルギー勾配)が常にゼロである $$ \frac{\partial E}{\partial Q} = 0 $$
- 特定の変位方向に対して局所 不安定状態(上に凸の放物線) であり、その変位方向にはエネルギーの座標に関する二次微分の値が負となる $$ \frac{\partial^2 E}{\partial Q^2} < 0 $$
- 振動解析すると、1つの振動モードの振動数のみが負の値になる
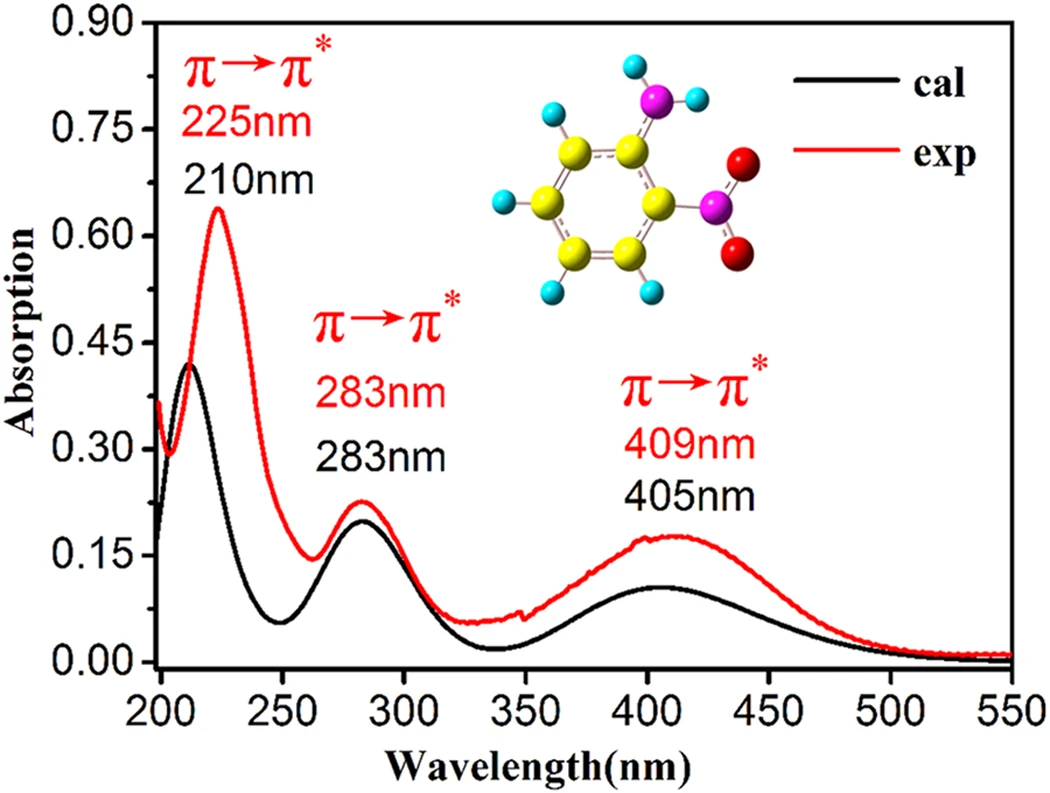
🟩 量子化学計算に基づく電子励起状態 💥 の解析
🤔 化合物の反応性について、熱や光など、化合物の特性以外の要因の影響は見ることは?
- 「光」については、化合物を光で励起した後の状態(励起状態)について、量子化学計算を用いて、その影響を調べることが可能です
- たとえば…
- 化合物が吸収・発光する光の波長 / 強度
- 光励起したあとの化合物の構造変化・反応過程
光の吸収とは?
- 光のエネルギーが分子を基底状態から励起状態に変えるエネルギーとして消費されるプロセス

- $E_{励起} - E_{基底} = \Delta E = h c / \lambda_{abs}$ に相当する光のエネルギーを分子が吸収し、基底 → 励起状態への電子遷移が起こる
- $h$: Planck 定数
- $c$:光の速度
分子の吸光・発光と基底・励起状態

- 吸光
- 基底($\mathrm{S_0}$)状態の最適構造 → 励起($\mathrm{S_n}$)状態
- つまり、量子化学計算に取り組むときに、分子の立体構造は、基底状態で最適化する必要がある
- 基底($\mathrm{S_0}$)状態の最適構造 → 励起($\mathrm{S_n}$)状態
- 発光
- 励起($\mathrm{S_n}$)状態の最適構造 → 基底($\mathrm{S_0}$)状態
- つまり、量子化学計算に取り組むときに、分子の立体構造は、励起状態で最適化する必要がある
- 励起($\mathrm{S_n}$)状態の最適構造 → 基底($\mathrm{S_0}$)状態
🎈 応用事例: 高効率な有機ELを設計したい
- 分子軌道のカタチを調べることでロジカルな設計が可能となった
- ➡ HOMO と LUMO の重なりを少なくすることで、$\mathsf{T_1}$ → $\mathsf{S_1}$ の項間交差(ISC)を促進する

🎈 応用事例: 環境応答性をもつ色素材料を設計したい
🎈 応用事例: 古代ホタルは何色に光るのか?
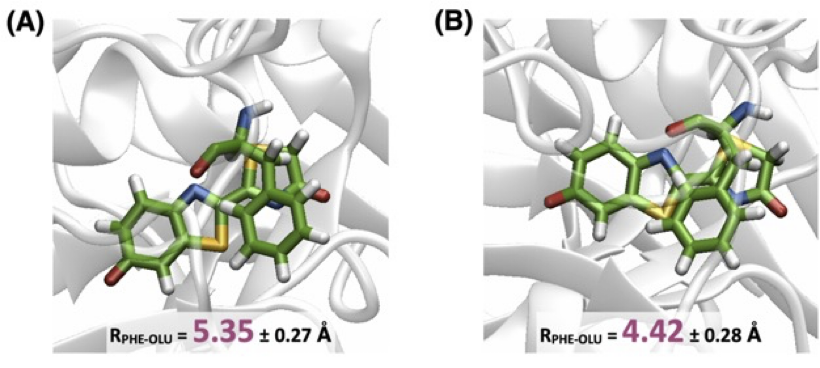
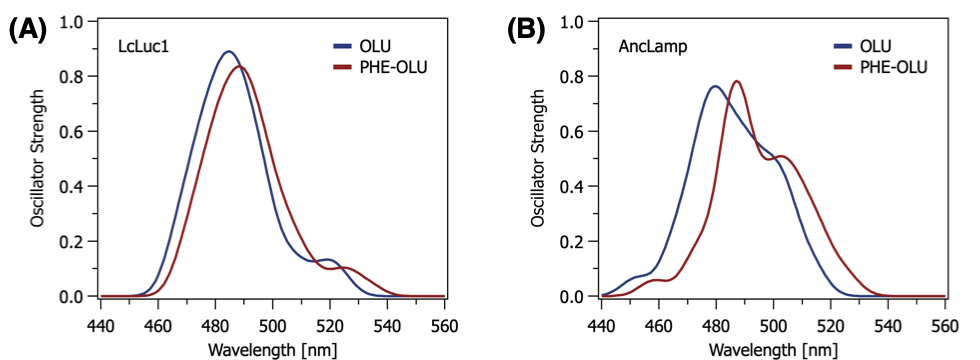
励起状態の計算方法
DFT を用いて励起状態を解析できる?
- DFT は、基底状態の計算に関しては、HF 法と同等のコストで、post HF 精度の結果が得られる可能性があります。
- DFT は、原子や分子の励起状態に関しても、時間依存(TD)の問題として扱うように拡張(TD-DFT)できます。
- TD-DFTは、化学発光 / 光触媒 / 太陽電池 / 光合成など、さまざまな分野で活用されています。
- ただし、TD-DFT を用いて励起状態を解析するときには、注意が必要な場合もあります。
Gaussian で TD-DFT を用いて励起状態を計算する

TD-DFTとは?
- 時間依存 Kohn-Sham 方程式は、時間依存 Schrödinger 方程式と同様に、次のように表すことができます:
$$ \hat{h}_i^\mathrm{KS} \phi_i^\mathrm{KS} = i\frac{\partial}{\partial t} \phi_i^\mathrm{KS} $$
線形応答理論に基づいて、時間依存 KS 方程式を解くと… $$ \begin{bmatrix} A & B \\ B^* & A^* \end{bmatrix} \begin{bmatrix} X \\ Y \end{bmatrix} = \omega \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} X \\ Y \end{bmatrix} $$
$\pm \omega$ の値が、励起 & 脱励起のエネルギーに対応します
行列 $\mathbf{B}$ を無視して上記の方程式を解く扱いのことを、Tamm-Dancoff 近似(TDA) といいます:
- $\mathbf{AX} = \omega \mathbf{X}$
- 遷移モーメントの定量性が悪くなる可能性があります
- 一方で、励起エネルギーの計算精度が改善されることがあります
TD-DFT のベンチマーク(汎関数依存性) 📊
- 領域分割 hybrid 型(長距離補正)を用いることで、計算精度が改善しています。
- 蛍光(fluorescence)の結果に関しては、ベンチマークに用いたデータが少ないので、信頼性に欠けるかもとのこと。
💻 実演:ホルムアルデヒドの電子励起状態の解析
🟩 量子化学計算に基づく溶媒 🥃 効果の解析
🤔 反応溶媒の選択の指標は得られるか?
- 反応溶媒を選択する際に何か指標となるような計算ができないか?
- 量子化学計算で目的物の選択性を向上させるためのヒントは?
- 溶液中での溶解度・溶解速度や、構造の取り方(イオン化の有無 / 単一分子 o r 複合体で溶解しているかなど)の予測は?
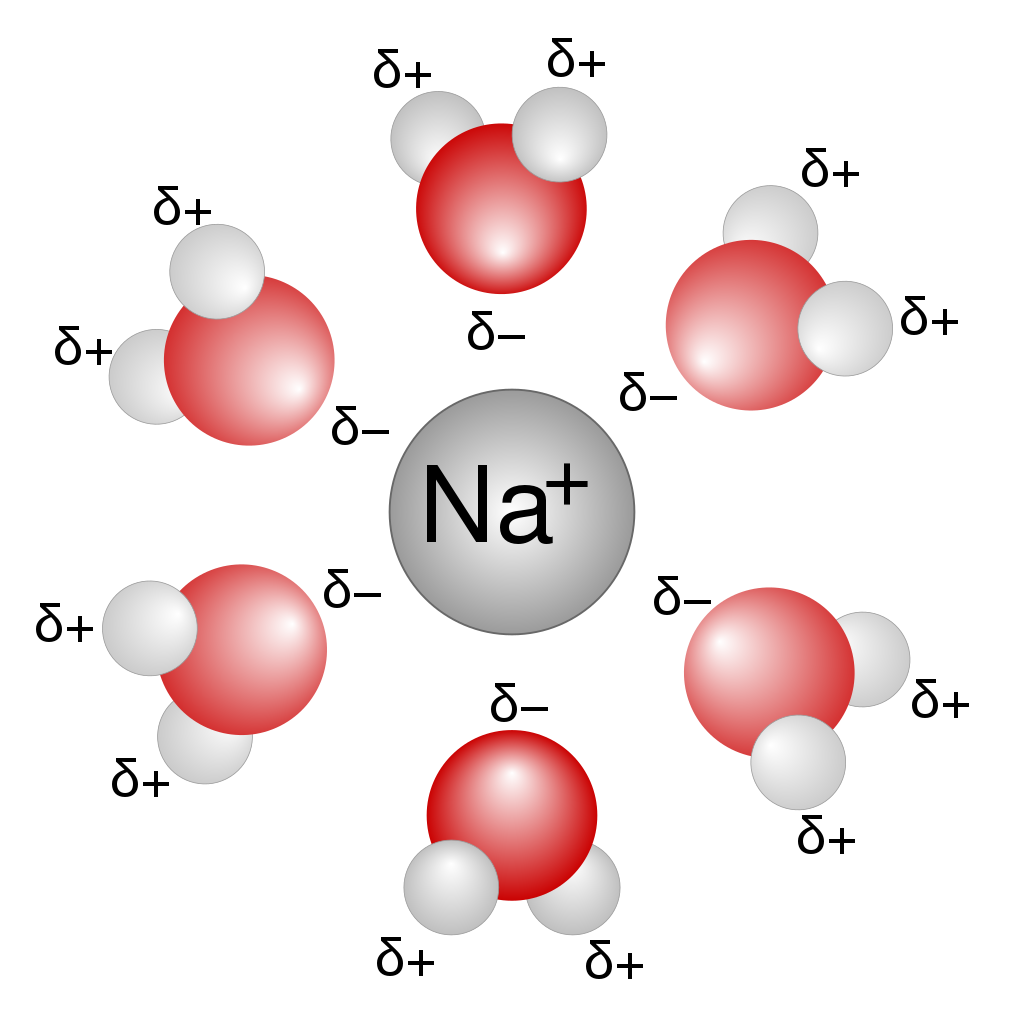
溶媒和とは
- 溶質分子が、静電気力や水素結合などによって結びつき取り囲むことで溶質が溶媒中に拡散する現象
溶媒効果とは?
- 化学において、反応性もしくは分子の会合に対して溶媒が及ぼす影響を指す
- 溶媒は溶解度、安定性、反応速度に影響を及ぼすため、適切な溶媒を選択することにより、化学反応を熱力学的・速度論的に制御できる
- 溶媒効果の例
- アセチルアセトンの互変異性に対する平衡定数: $$ K_\mathrm{keto-enol} = \mathrm{\frac{[enol]}{[keto]}} $$

- ある可逆的な反応過程 $A$ について、対応する平衡定数 $K$ とギブス自由エネルギー変化 $\Delta G$ の関係
$$ \Delta G = -RT \ln K $$
- $R$:気体定数($= k_\mathrm{B} N_\mathrm{A} = 8.314,462 \; \mathrm{J \; K^{-1} \; mol^{-1}}$)
- $T$:温度(300 K)
| 溶媒の種類 | keto-enol 平衡定数 | ギブス自由エネルギー変化 |
|---|---|---|
| 気相 | 11.7 | -6.12 |
| 水 | 0.23 | 3.67 |
| ジクロロメタン | 4.2 | -3.58 |
| エタノール | 5.8 | -4.39 |
| テトラヒドロフラン | 7.2 | -4.93 |
| ベンゼン | 14.7 | -6.70 |
| シクロヘキサン | 42 | -9.32 |
量子化学計算で溶媒効果を考慮するには
溶媒分子を露わに考慮する(explicit solvation model)
溶媒分子を分極する連続誘電体として扱う(implicit solvation model)
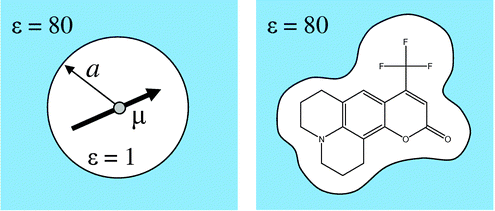
- 左:Debye-Onsager モデル
- 右:連続誘電体モデル
Gaussian で溶媒効果を考慮する

溶媒効果の具体例
- エタノールについて、さまざまな溶媒に対する溶媒和エネルギー($\Delta E_\mathrm{sol} = E_\mathrm{sol} - E_\mathrm{gas}$)を量子化学計算に基づいて解析する
B3LYP/6-31G(d)
| 溶媒の種類 | RHF Energy (Hartree) | エネルギー差 (kcal/mol) |
|---|---|---|
| 孤立気相 | -154.075744507 | |
| Water | -154.081212575 | -3.431 |
| Acetonitrile | -154.081069207 | -3.341 |
| Cyclohexane | -154.077836155 | -1.312 |
🤔 質疑応答 16:00 〜 16:30
🙇 さいごに
共同研究・技術相談 🗣️
- 計算化学(分子動力学・量子化学・機械学習)に関して、共同研究や技術相談をお受けしています
- 興味・関心を持っていただけましたら、山本までお問い合わせください
- 連絡先
- norifumi.yamamoto (at) p.chibakoudai.jp
- (at) を @ に変えてください
- norifumi.yamamoto (at) p.chibakoudai.jp
このノートは、現在、アドレス(URL)を知っている人だけが閲覧できる「限定共有」版です。 このページの URL は、関係者以外には秘密にしてください。
![Solov'yov, et al. (2012)]](https://gyazo.com/48f5e3d868003070ac0fbf8dd02f1e06.png)