エチレンの円錐交差構造を探索する
はじめに
分子が比較的高いエネルギーの波長領域(近赤外〜可視・紫外領域)の光を吸収すると、この分子の電子状態が、エネルギー的に最も安定な(電子)基底状態から、エネルギー的に不安定な(電子)励起状態に変化します。
このような光吸収の後、励起状態となった分子は、吸収したエネルギーを光として放出しながら基底状態に戻る場合があります。このように、励起された分子が「光の放出をともなって基底状態に戻る」ことを発光といいます。
一方で、分子の立体構造が変化しながら励起状態と基底状態の間のエネルギー差が段々と小さくなり、最終的に、そのエネルギー差がゼロになってしまう場合があります。この「電子状態間のエネルギー差がゼロとなって互いに交差する」ことを円錐交差といいます。
基底状態と励起状態が円錐交差する地点に辿り着いたとき、この分子は、光を放出しないで基底状態に戻ることができます。このように、励起状態となった分子が「光の放出をともなわずに基底状態に戻る」ことを無輻射遷移、あるいは、非断熱遷移といいます。
非断熱遷移は、光照射によって分子の形を変える光異性化反応などで重要な役割を果たし、さまざまな機能性分子が多彩で巧みな機能を発現するための源にもなっています。したがって、ある分子の光化学反応を解析するときに、光励起後に到達するかもしれない円錐交差の地点を探索し、その立体構造を調べたり、非断熱遷移の起こりやすさを調べたいと思うことがしばしばあります。
このノートでは、エチレン(CH2=CH2)を例として、その基底(S0)状態と励起(S1)状態が交差する円錐交差構造を探索する手順を解説します。量子化学計算プログラムには GAMESS を用います。
このノートで説明する出力ファイルが GitHub にあります。また、Google Colab にアクセスすると、プログラミング言語 Python を用いて、グラフの作成などを実際に実行することもできます(Colab の利用には、Google アカウントが必要です)。
円錐交差を探索する手順
S0 状態の最小エネルギー構造を探索する
はじめに、エチレンの基底(S0)状態で最も小さいポテンシャルエネルギーを持つ構造を探索してみましょう。このような構造のことを、最小エネルギー構造、あるいは、最適構造といいます。そして、最小エネルギー構造を探索する計算のことを構造最適化(Geometery Optimization)といいます。
構造最適化をおこなうときの GAMESS の入力ファイルは、次のようになります。電子状態の計算には、密度汎関数(DFT)法を用います。汎関数は BHHLYP、基底関数には 6-31G(d) です。
$CONTRL
RUNTYP=OPTIMIZE
SCFTYP=RHF
DFTTYP=BHHLYP
ICHARG=0
MULT=1
COORD=UNIQUE
$END
$STATPT
NSTEP=100
$END
$SYSTEM
MWORDS=128
$END
$BASIS
GBASIS=N31 NGAUSS=6 NDFUNC=1
$END
$DATA
C2H4
C1 1
C 6 0.00000000 0.00000000 0.00000000
C 6 -1.31000000 0.00000000 0.00050000
H 1 -1.85000000 -0.93530000 -0.00050000
H 1 -1.85000000 0.93530000 0.00180000
H 1 0.54000000 0.93530000 0.00100000
H 1 0.54000000 -0.93530000 0.00320000
$END計算の結果得られた GAMESS の出力ファイルは こちら 。出力ファイルから構造最適化に伴う全エネルギーの変化を読み取り、グラフとして表してみましょう。Python を使ってこのようなグラフを作る方法を Google Colab で紹介しています。
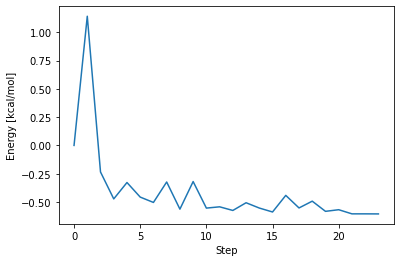
このグラフは、縦軸が初期構造をゼロとしたときの全エネルギーの変化、横軸が構造最適化の手続きを繰り返した回数(ステップ数)を示しています。これを見ると、構造最適化の手続きが繰り返されるごとに、この系の全エネルギーが徐々に減少していることが分かります。
また、ある構造における系の全エネルギー($E$)を座標($R$)で微分したエネルギー勾配($\partial E / \partial R$)の値についても、構造変化に伴ってどのように変化するのかを見てみましょう。
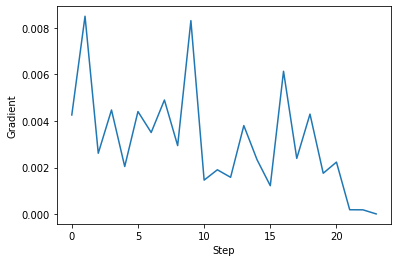
これを見ると、構造最適化の手続きが繰り返されたとき、エネルギー勾配の値が必ずしも順調に小さくなっていくわけではありませんが、おおむね、その値がゼロとなる地点に向かっていることが分かります。
全エネルギーの変化とエネルギー勾配の値が十分に小さくなったとき、構造状態が局所的な安定点(最適構造)に到達していると判断することができます。この計算では、構造最適化の手続きを 23 回繰り返した後、プログラムが「これ以上計算してもエネルギーは小さくならないだろう」と判断し、「この分子の最適構造が見つかった」と宣言して計算を終了しています。
エチレンは炭素-炭素間にπ結合を持っています。これらの炭素原子はsp2混成軌道を形成していますので、この炭素にσ結合でつながった水素原子を含めて、全ての原子が同一平面上にあるような平面構造が最も安定な状態となっています。
以上が、エチレンの S0状態の最小エネルギー構造を探索する構造最適化の手続きでした。
S0 → Sn 励起状態のエネルギーを解析する(TD-DFT法)
分子に光を照射すると、基底状態のエネルギー($E_0$)と励起状態のエネルギー($E_1$)の差 $\Delta E = E_1 − E_0$ に相当する光のエネルギーを分子が吸収し、基底状態 → 励起状態への遷移がおこります。

そこで次に、エチレンがS0状態の最小エネルギー構造であるときの励起状態のエネルギー$E_1(R_0)$を求めて、分子が吸収する光のエネルギーを解析してみましょう。
構造最適化をおこなうための GAMESS の入力ファイルは、次のようになります。電子励起状態の解析には、時間依存密度汎関数(Time-Dependent Density Functional Theory; TD-DFT)法を用います。指定する汎関数と基底関数は、基底状態の構造最適化で用いたものと同じ BHHLYP と 6-31G(d) です。
$CONTRL
RUNTYP=ENERGY
TDDFT=EXCITE
SCFTYP= RHF
DFTTYP=BHHLYP
ICHARG=0
MULT=1
COORD=UNIQUE
$END
$TDDFT
NSTATE=5
$END
$SYSTEM
MWORDS=128
$END
$BASIS
GBASIS=N31 NGAUSS=6 NDFUNC=1
$END
$DATA
C2H4
C1 1
C 6 0.00000000 0.00000000 0.00000000
C 6 -1.32029884 0.00001048 -0.00023551
H 1 -1.88916197 -0.91657892 -0.00030266
H 1 -1.88916423 0.91658755 -0.00032712
H 1 0.56876188 0.91665251 0.00010461
H 1 0.56877229 -0.91667652 0.00003663
$END計算で得られた GAMESS の出力ファイルは こちら 。出力されたファイルから、各励起状態のエネルギーに関わる部分を抜き出してみましょう。
抜き出した部分の上から3行目(0 Aで始まる1行)には基底(S0)状態についての情報、4行目(1 Aで始まる1行)には第一励起(S1)状態についての情報がそれぞれ表示されています。
STATE ENERGY EXCITATION TRANSITION DIPOLE, A.U. OSCILLATOR
0 -> HARTREE EV X Y Z STRENGTH
0 A -78.5299343886 0.000
1 A -78.2220204978 8.379 1.3847 -0.0000 0.0003 0.3936
2 A -78.2003758061 8.968 0.0003 -0.0000 -0.0000 0.0000
3 A -78.1739060826 9.688 0.0000 -0.0000 0.0413 0.0004これを見ると、S0 状態のエネルギーが $E_0$ = -78.5299 Hartree、S1 状態のエネルギーが $E_1$ = -78.2220 Hartree であることから、その差は $\Delta E = E_1 − E_0 =$ 0.308 Hartree であることが分かります。
Hartree という物理定数は、量子化学計算でよく用いられる原子単位系(atomic unit)で、エネルギーを表す単位として使われます。光化学の分野では、エレクトロンボルト(eV)という単位を用いることが多いです。1 Hartree は 27.2114 eV に相当するので、このエネルギー差は $\Delta E$ = 8.379 eV となります。
S1 状態の最小エネルギー構造を探索する
次に、S0 → S1 状態間のエネルギーに相当する波長の光をエチレンに照射したとして、この分子が S1 状態に変わった(遷移した)後の振る舞いを調べてみます。
まずは、S1 状態におけるエチレンの最適構造を探索してみます。電子励起状態の解析には、先ほどと同じ、TD-DFT 法を用います。汎関数と基底関数もこれまでと同様、BHHLYP と 6-31G(d) です。初期構造としては、S0 状態で求めた最適構造を指定しています。入力ファイルは、次のようになります。
$CONTRL
RUNTYP=OPTIMIZE
TDDFT=EXCITE
SCFTYP= RHF
DFTTYP=BHHLYP
ICHARG=0
MULT=1
COORD=UNIQUE
$END
$STATPT
NSTEP=100
$END
$TDDFT
NSTATE=3
IROOT=1
$END
$SYSTEM
MWORDS=128
$END
$BASIS
GBASIS=N31 NGAUSS=6 NDFUNC=1
$END
$DATA
C2H4
C1 1
C 6 0.00000000 0.00000000 0.00000000
C 6 -1.32029900 0.00001000 -0.00023600
H 1 -1.88916200 -0.91657900 -0.00030300
H 1 -1.88916400 0.91658700 -0.00032700
H 1 0.56876200 0.91665200 0.00010500
H 1 0.56877200 -0.91667600 0.00003700
$ENDGAMESS の出力ファイルは こちら 。出力されたファイルから構造最適化に伴う S0 状態と S1 状態のエネルギー変化を読み取り、グラフとして表してみましょう。
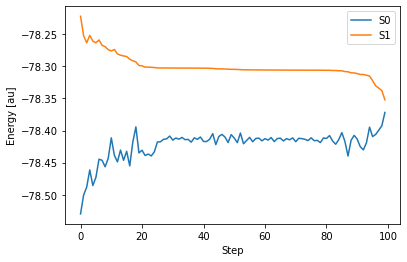
これをみると、構造最適化の手続きが繰り返されるごとに、S1 状態のエネルギーが徐々に減少していく一方で、S0 状態のエネルギーは徐々に増加していくことが分かります。そして最終的に、2つの状態がエネルギー的にかなり近接していることが分かります。
それでは、この構造最適化にともなう立体構造の変化を見てみましょう。
これを見ると、平面構造から出発したエチレンは、2つの炭素間の C-C 結合が回転し、2つのCH2部位が互いに捻れた構造にたどり着いています。最終的にたどり着いた構造の性質を詳しく見るために、GAMESS の出力ファイルから、各励起状態のエネルギーに関わる部分を抜き出してみましょう。
STATE ENERGY EXCITATION TRANSITION DIPOLE, A.U. OSCILLATOR
0 -> HARTREE EV X Y Z STRENGTH
0 A -78.3719301502 0.000
1 A -78.3522429634 0.536 0.3305 0.0034 -0.0310 0.0014
2 A -78.1089517593 7.156 0.1238 0.1346 -0.0360 0.0061
3 A -78.1045447013 7.276 -0.1739 0.2990 -0.0746 0.0223抜き出した部分の上から3行目(0 Aで始まる1行)にS0状態の情報、4行目(1 Aで始まる1行)にS1状態の情報がそれぞれ表示されています。
4行目を見ると、S0 状態と S1 状態のエネルギー差は $\Delta E$ = 0.536 eV であり、かなり近接していることが分かります。この 0.536 eV という値は、波長に変換すると 2314 nm になります。人間の目で認識できる光の波長領域は 400 〜 800 nm 程度なので、もしこのエネルギー差に相当する「光」が放出されたとしても、私たちには「見る」ことができません。しかし、2つの状態のエネルギーが等しいと判断するには大きすぎる値なので、「円錐交差」しているとはまだいえません。
つまり、S0 状態と S1 状態のエネルギー差がゼロとなる円錐交差を探索しようとするときに、まずは S1 状態の構造最適化をやってみることでゴール地点には近づくだろうと想定できるのですが、それだけでは不十分なようです。
そこで次に、GAMESS に実装されている機能を用いて、円錐交差構造を効率的に探索してみましょう。
円錐交差を解析するときに注意するべきこと
円錐交差構造を探索しようとするとき、注意するべきことがあります。それは、基底 S0 状態と励起 S1 状態のエネルギー差がゼロとなる円錐交差の状態を解析しようとする場合、普通の TD-DFT 計算を使うことができないということです。
試しに、GAMESS で TD-DFT 法を使って円錐交差構造を探索してみました。円錐交差構造を探索するための具体的なやり方は、後ほど説明します。この計算で得られた 出力ファイル をもとに、S0 状態と S1 状態のエネルギー変化をグラフに表してみます。
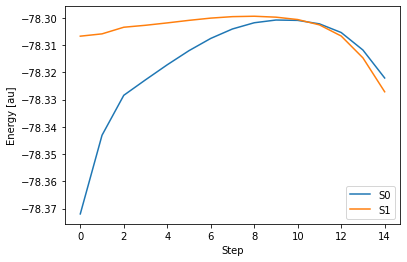
この場合、計算を始めて14 ステップ目で、自己無撞着場(Self Consistent Field; SCF)計算という、シュレディンガー方程式を近似的に解くための手続きが収束せず、異常終了してしまいます。これは、この計算が途中からS0 状態と S1 状態が近接し、エネルギー差がゼロとなってお互いを区別できなくなってしまう(このような状態を縮退と言います)ことに原因があります。
このような問題を回避するためによく用いられるのが、スピン反転(Spin-Flip; SF) TD-DFT 法です。たとえば、参照状態として三重項 T1 状態を用いて、スピンを反転させて遷移した状態として基底 S0 状態と励起 S1 状態を準備することにします。
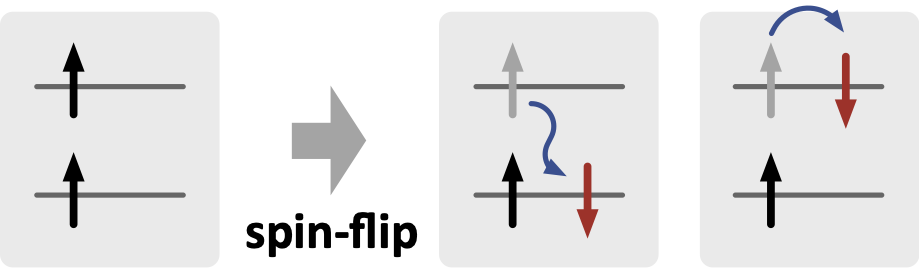
すると、この S0 と S1 の2つの状態のエネルギー差がゼロとなって区別ができなくなったとしても、参照状態である T1 とこの2つの状態にエネルギー的な大小関係があって互いに区別ができるのであれば、問題なく励起状態の解析を続けることができるはずです。
S0 → Sn 励起状態のエネルギーを解析する(SF-TD-DFT 法)
GAMESS には、SF-TD-DFT 法が実装されています。円錐交差構造を探索するための準備として、SF-TD-DFT 法を用いて、エチレンの励起エネルギーを解析してみましょう。汎関数と基底関数は、これまでと同様、BHHLYP/6-31G(d) です。入力する構造は、TD-DFT 法で求めた S1 状態の最小エネルギー構造です。入力ファイルは、次のようになります。
$CONTRL
RUNTYP=ENERGY
TDDFT=SPNFLP
SCFTYP=ROHF
DFTTYP=BHHLYP
ICHARG=0
MULT=3
COORD=UNIQUE
$END
$SYSTEM
MWORDS=128
$END
$BASIS
GBASIS=N31 NGAUSS=6 NDFUNC=1
$END
$TDDFT
NSTATE=3
TAMMD=.T.
$END
$DATA
C2H4
C1 1
C 6 0.00000000 0.00000000 0.00000000
C 6 -1.39387838 -0.02023373 0.05708308
H 1 -2.02405816 -0.69695202 0.61316012
H 1 -1.99290168 0.59587111 -0.65717732
H 1 0.70303672 0.57666607 0.58418458
H 1 0.52478100 -0.71663905 -0.63734377
$END計算で得られた GAMESS の出力ファイルは こちら 。出力されたファイルから、各励起状態のエネルギーに関わる部分を抜き出してみましょう。
STATE ENERGY EXCITATION S-SQUARED
0 NEGATIVE ROOT(S) FOUND.
0 A -78.4266430282 0.000 (REFERENCE STATE)
1 A -78.4021583898 0.666 0.1132
2 A -78.4019622431 0.672 1.8930
3 A -78.3146323372 3.048 0.0646このような SF-TD-DFT 計算で得られた出力ファイルを読み解こうとするときには、S-SQUAREDという部分に注意する必要があります。S-SQUARED とは、全
スピン角運動量
$S$ の二乗 $S^2$ に対する期待値 $\langle S^2 \rangle$ のことです。スピン
多重度
を $n = 2S + 1$ とすると、次のように表すことができます。
$$\langle S^2 \rangle = S (S+1) = \frac{n-1}{2} \left(\frac{n-1}{2} + 1\right)$$
このことから、スピン多重度が一重項である状態($n$ = 1)のときは $\langle S^2 \rangle$ = 0、二重項である状態($n$ = 2)のときは $\langle S^2 \rangle$ = 0.75、三重項である状態($n$ = 3)のときは $\langle S^2 \rangle$ = 2 となるはずです。つまり $\langle S^2 \rangle$ の値は、対応する電子状態のスピン多重度がどの状態であるかを判断するための手がかりになります。
ある分子について、基底状態における電子配置が閉殻構造(全ての占有軌道の電子数が2個)である一重項状態の場合、通常の TD-DFT 法で計算すると、一重項状態や三重項状態の $\langle S^2 \rangle$ の値は、上記で計算してみたとおりに、0 や 2 という整数値になります。
一方、SF-TD-DFT 法で計算した結果を見ると、$\langle S^2 \rangle$ が 0.1132(State 1), 1.8930(State 2), 0.0646(State 3)のように、期待とは異なる値になってしまっています。これは、一重項や三重項が混ざり合ってしまい、正しいスピン状態が得られていないことを意味しています。このような問題のことを スピン汚染 といいます。
SF-TD-DFT 計算では、このスピン汚染が大きくなりがち。したがって、S-SQUARED の値に基づいて、各状態がどのスピン多重度に対応するのか、判断する必要があります。先ほどの結果については、S-SQUARED の値を参考にすると、各状態は次のように帰属できそうです。
| STATE | S-SQUARED | 帰属 | エネルギー差(eV) |
|---|---|---|---|
| 0 A | (Reference) | T1 | -0.666 |
| 1 A | 0.1132 | S0 | 0.000 |
| 2 A | 1.8930 | T2 | 0.005 |
| 3 A | 0.0646 | S1 | 2.382 |
このように、1 Aとラベルされていたものは S0 状態、3 Aとラベルされていたものは S1 状態と考えることができそうです。ここで、S0 状態をゼロ点として、他の状態とのエネルギー差を調べてみましょう。すると、S0/S1 状態間のエネルギー差は 2.382 eV であることが分かります。次に、この2つの状態のエネルギー差がゼロとなる円錐交差の構造を探索していきましょう。
S0/S1 状態間の円錐交差構造を探索する
SF-TD-DFT 法を用いて、S0 状態と S1 状態のエネルギー差がゼロとなる円錐交差構造を探索してみましょう。汎関数と基底関数は、これまでと同様、BHHLYP/6-31G(d) です。入力する構造は、TD-DFT法で求めた S1 状態の最小エネルギー構造です。入力ファイルは、次のようになります。
$CONTRL
RUNTYP=CONICAL
TDDFT=SPNFLP
SCFTYP=ROHF
DFTTYP=BHHLYP
ICHARG=0
MULT=3
COORD=UNIQUE
$END
$SYSTEM
MWORDS=128
$END
$BASIS
GBASIS=N31 NGAUSS=6 NDFUNC=1
$END
$CONICL
IXROOT(1)=1,3
$END
$TDDFT
NSTATE=3
TAMMD=.T.
$END
$DATA
C2H4
C1 1
C 6 0.00000000 0.00000000 0.00000000
C 6 -1.39387800 -0.02023400 0.05708300
H 1 -2.02405800 -0.69695200 0.61316000
H 1 -1.99290200 0.59587100 -0.65717700
H 1 0.70303700 0.57666600 0.58418500
H 1 0.52478100 -0.71663900 -0.63734400
$END計算で得られた GAMESS の出力ファイルは こちら 。出力されたファイルから、各状態のエネルギー変化をグラフで表してみます。
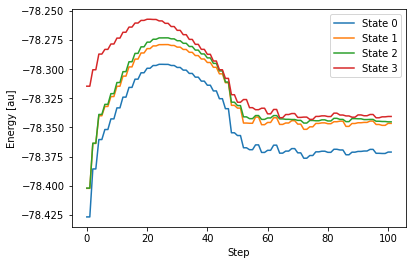
先ほど、State 1 が S0 状態、State 3 が S1 状態であると判断しました。グラフで表したエネルギー変化をみると、この2つの状態は、計算を始めるとエネルギー的に徐々に近接していて、40ステップを過ぎたあたりでほぼ交差しているにも見えます。しかし、その後は再びエネルギー差が大きくなります。繰り返し計算の上限値である 100 ステップに至っても、State 1 と State 3 のエネルギー差は 0.83 eV と大きいまま。つまりこの計算では、2つのエネルギー状態が交差する(エネルギー差がゼロになる)という円錐交差に辿り着くことができませんでした。なぜでしょう。
前に説明したように、SF-TD-DFT 法を用いるとき、$\langle S^2 \rangle$ の値を気にする必要があります。そこで、今回の計算にともなって $\langle S^2 \rangle$ の値がどのように変化したのかを調べてみました。
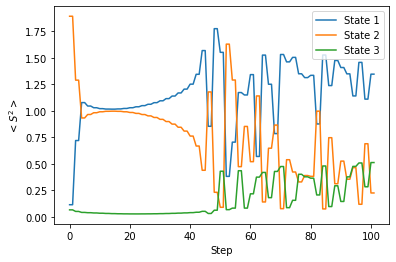
この計算を始める前、$\langle S^2 \rangle$ の値に基づいて、State 1 が S0 状態、State 3 が S1 状態であると帰属していました。しかし上記のグラフを見るとと、計算が始まるとすぐに、State 1 の $\langle S^2 \rangle$ が 0.1 から 1 程度まで急激に大きくなっていることが分かります。これは計算開始直後、State 1(計算前には S0 であると帰属)と State 2(計算前には T2 であると帰属)がエネルギー的に近接し、2つの状態間でスピン混入が起こるためだと考えられます。その後しばらくすると、20ステップあたりから、State 1 の $\langle S^2 \rangle$ の値は徐々に大きく、State 2 の $\langle S^2 \rangle$ の値は徐々に小さくなっていくことが分かります。
40ステップ以降、State 1〜3 の $\langle S^2 \rangle$ の値は大きく上下し始めます。これは、3つの状態がエネルギー的に近接し、スピン混入がさらに大きくなっているためだと考えられます。このような状況で各状態のスピン多重度を判断するのは難しいのですが、大まかには、$\langle S^2 \rangle$ が1.25 付近である State 1 を三重項状態、$\langle S^2 \rangle$ が 0.5 付近である State 2 と State 3 を一重項状態だと帰属することができそうです。つまり、 この計算を始める前には State 1 が S0 状態であると考えていたのですが、計算が進むうちに状態間の入れ替わりが起こっています。
S0/S1 状態間の円錐交差構造を探索する(2回目)
さて、先ほど取り組んだ計算では、電子状態の入れ替わりが起こってしまったことで、エチレンの円錐交差構造に辿り着くことができませんでした。このことから、次に、ターゲットとして指定する状態を、State 2 と State 3 に設定し直して、再度計算してみます。汎関数と基底関数は、これまでと同様、BHHLYP/6-31G(d) です。入力する構造は、1回目の計算で辿り着いた構造です。入力ファイルは、次のようになります。
$CONTRL
RUNTYP=CONICAL
TDDFT=SPNFLP
SCFTYP=ROHF
DFTTYP=BHHLYP
ICHARG=0
MULT=3
COORD=UNIQUE
$END
$SYSTEM
MWORDS=128
$END
$BASIS
GBASIS=N31 NGAUSS=6 NDFUNC=1
$END
$CONICL
IXROOT(1)=2,3
$END
$TDDFT
NSTATE=3
TAMMD=.T.
$END
$DATA
C2H4
C1 1
C 6 0.00000000 0.00000000 0.00000000
C 6 -1.33723876 -0.30093935 0.13764264
H 1 -1.78391968 -1.11038634 0.75036359
H 1 -2.09508746 0.14953750 -0.49933204
H 1 0.61067046 -0.03539838 0.90583015
H 1 0.14815501 -1.10406642 -0.28386137
$END計算で得られた GAMESS の出力ファイルは こちら 。出力されたファイルから、各状態のエネルギー変化をグラフで表してみます。
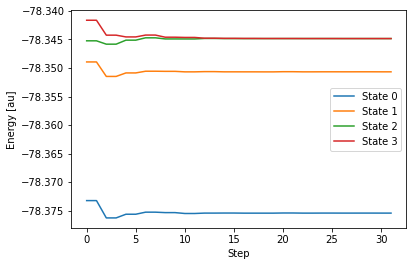
これを見ると、計算を始めて 10 ステップ後には、ターゲットとして指定した State 2 と State 3 がエネルギー的に近接し、ほぼ縮退していることが分かります。この計算では、30ステップの後、エネルギー差などをもとにプログラムが「円錐交差に到達した」と判断して、無事に終了しています。
念のため、このときの $\langle S^2 \rangle$ の変化についてもグラフで表してみます。
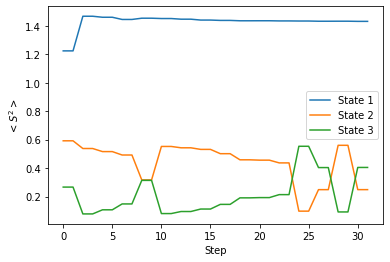
これを見ると、ターゲットとして指定した State 2 と State 3 は $\langle S^2 \rangle$ の値が 0.1 〜 0.6 の間で上下してはいますが、State 1 と比べて十分に小さくなっていることが分かります。
最終的に辿り着いたエチレンの円錐交差を見てみましょう。
これを見ると、エチレンの CH2 部位について、1つは平面となっています。もう1つの CH2 部位は折れ曲がっていて、2つの炭素原子と2つの水素原子に注目すると、これらを頂点とする三角錐に見える構造となっていることが分かります。このように分子の立体構造が「三角錐」に変化することを、 ピラミッド化(pyramidalization) ということがあります。
以上のことから、エチレンの円錐交差構造は、中央の C-C 結合が回転し、CH2 部位がピラミッド化した状態であることが明らかとなりました。
さいごに
このような円錐交差構造の探索は、機能性色素材料を解析する上で、重要な手がかりとなります。たとえばヤマラボで取り組んでいる「凝集誘起発光」現象の解析でも、このような計算をおこなっています。関連する論文をいくつかご紹介しておきますね。
- Norifumi Yamamoto, Free energy profile analysis to identify factors activating the aggregation-induced emission of a cyanostilbene derivative , Phys. Chem. Chem. Phys., Vol. 23, pp. 1317-1324 (2021)
- Norifumi Yamamoto, Free energy profile analysis for the aggregation-induced emission of diphenyldibenzofulvene , J. Phys. Chem. A, Vol. 124, pp. 4939-4945 (2020)
Appendix
TD-DFT と SF-TD-DFT の比較
TD-DFT
TD-DFT は、基底状態から励起状態への遷移エネルギーを計算するために使用される手法で、Kohn-Sham 軌道を基に励起エネルギーを導出します。TD-DFT の計算は、次のような行列方程式を解くことから始まります。
$$ \begin{pmatrix} A & B \\ B^* & A^* \end{pmatrix} \begin{pmatrix} X \\ Y \end{pmatrix} = \begin{pmatrix} \omega & 0 \\ 0 & -\omega \end{pmatrix} \begin{pmatrix} X \\ Y \end{pmatrix} $$
$\omega$ は励起エネルギー、行列 $A$ と $B$ はそれぞれ次のように定義されます。
$$ A_{ia,jb} = \delta_{ij} \delta_{ab} (\epsilon_{a} - \epsilon_{i}) + 2(ia | jb) - \alpha_{X} (ij | ab) + (1 - \alpha_{X})(ia | f_{\text{XC}} | jb) $$
$$ B_{ia,jb} = 2(ia|bj) - \alpha_X (ib|aj) + (1 - \alpha_X)(ia|f_{\text{XC}}|bj) $$
ここで…
- $\epsilon_a$ : 仮想軌道 $a$ のエネルギー
- $\epsilon_i$ : 占有軌道 $i$ のエネルギー
- $(ia|jb)$ : クーロン相互作用を表す双対積分
- $\alpha_X$ : hybrid 汎関数における Hartree-Fock (HF) の寄与を制御するパラメータ
Tamm-Dancoff 近似 (TDA)
TD-DFT では、しばしば Tamm-Dancoff 近似(TDA) が用いられます。TDA では、行列 $B$ を無視して計算が簡略化されて、行列方程式は次のようになります。
$$ A X_{\text{TDA}} = \omega_{\text{TDA}} X_{\text{TDA}} $$
SF-TD-DFT
spin-flip 法の基本的な考え方は、UHF 基底状態から、スピン多重度が $M_{S_{\text{SF}}} = M_{S_{\text{UHF}}} - 1$ となる状態への遷移を考慮することです。この場合の行列方程式は、TD-DFT をもとに、α軌道からβ軌道へのスピン反転に伴う遷移のみを考慮するため、行列 $A^{\text{SF}}$ の構成は次のようにシンプルになります:
$$ A_{\alpha i,\beta j}^{\text{SF}} = \delta_{ij} \delta_{\alpha \beta} ( \epsilon_\alpha - \epsilon_i ) - \alpha_X (ij|ab) $$
ここで $\alpha_X$ は HF の寄与を制御するパラメータ。HF に基づくエネルギー項が重要になります。したがって、SF-TD-DFT 計算に取り組む場合には、通常、BHHLYP のように、HF の寄与が大きい hybrid 型汎関数を選択することが推奨されます。
円錐交差を解析するためのプログラム
このノートでは、無料で使える代表的な量子化学計算プログラムパッケージの GAMESS を用いて、SF-TD-DFT を用いて分子の円錐交差構造を探索する方法を紹介しました。
GAMESS の他にも、SF-TD-DFT に基づく円錐交差構造の探索が可能なプログラムパッケージがいくつかあります。今のところ私が知っているのは、次の通りです:
量子化学計算の分野で最も有名な Gaussian
にも、構造最適化計算にConicalというオプションがあります。このオプションを使う(Opt=Conical)と、state-averaged CASSCF という手法を用いて、円錐交差構造の探索が可能です。
CASSCF は SF-TD-DFT に比べて、計算コストの高さや設定の難しさがあるのですが、代表的な量子化学計算プログラムの Gaussian で実行できるという利点は大きいかと思います。
